Teoremas do isomorfismo
En matemáticas, en concreto álxebra abstracta, os teoremas do isomorfismo (tamén coñecidos como Teoremas de isomorfismo de Noether) son teoremas que describen a relación entre cocientes, homomorfismos e, subobxectos. Existen versións dos teoremas para grupos, aneis, espazos vectoriais, módulos, Álxebras de Lie, e outras estruturas alxébricas. En álxebra universal, os teoremas de isomorfismo poden ser xeneralizados ao contexto de álxebras e congruencias.
Historia
[editar | editar a fonte]Os teoremas do isomorfismo foron formulados nalgunha xeneralidade para homomorfismos de módulos por Emmy Noether no seu artigo Abstrakter Aufbau der Idealtheorie en alxébrica Zahl - Und Funktionenkörpern, que foi publicado en 1927 en Mathematische Annalen. As versións menos xerais destes teoremas pódense atopar no traballo de Richard Dedekind e documentos anteriores de Noether.
Tres anos despois, B. l. van der Waerden publicou a súa influente Moderne Algebra, o primeiro libro de texto de álxebra abstracta que levou unha aproximación a este tema en grupos-aneis-corpos. Van der Waerden utilizou as conferencias de Noether sobre teoría de grupos e Emil Artín sobre álxebra, así como un seminario realizado por Artin, Wilhelm Blaschke, Otto Schreier, e o propio van der Waerden sobre ideais como as principais referencias.
Imos ver os teoremas de isomorfismo referidos aos grupos. Os teoremas refírense pola orde ou as veces polas letras A, B e C.
Primeiro teorema do isomorfismo
[editar | editar a fonte]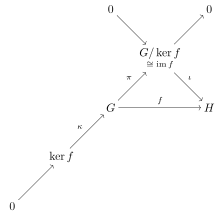
Sexan G e H grupos, e sexa f : G → H un homomorfismo. Entón:
- O kernel de f é un subgrupo normal de G.
- A imaxe de f é un subgrupo de H.
- A imaxe de f é isomorfa ao grupo cociente G / ker(f).
En particular, se f é sobrexectivo entón H é isomorfo a G / ker(f).
Segundo teorema do isomorfismo
[editar | editar a fonte]
Sexa un grupo. Sexa un subgrupo de , e sexa un subgrupo normal de . Entón cúmprese o seguinte:
- O produto é un subgrupo de .
- O subgrupo é un subgrupo normal de .
- A intersección é un subgrupo normal de .
- Os grupos cocientes e son isomorfos.
Tecnicamente, non é necesario que sexa un subgrupo normal, sempre que sexa un subgrupo do normalizador de en . Neste caso, non é un subgrupo normal de mais é aínda un subgrupo normal do produto .
Unha aplicación do segundo teorema do isomorfismo é identificar os grupos lineares proxectivos, por exemplo, o grupo sobre a liña proxectiva complexa comeza facendo , o grupo de matrices complexas 2 × 2 invertíbeis, , o subgrupo de matrices de determinante 1, e o subgrupo normal de matrices escalares , con eses grupos temos , onde é a matriz identidade e, . Entón o segundo teorema do isomorfismo afirma que:
Terceiro teorema do isomorfismo
[editar | editar a fonte]Sexa un grupo, e un subgrupo normal de . Entón
- Se é un subgrupo de tal que , entón ten un subgrupo isomorfo a .
- Cada subgrupo de é da forma para algún subgrupo de tal que .
- Se é un subgrupo normal de tal que , entón ten un subgrupo normal isomorfo a .
- Cada subgrupo normal de é da forma para algún subgrupo normal de tal que .
- Se é un subgrupo normal de tal que , entón o grupo cociente é isomorfo a .
As catro primeiras afirmacións adoitan subsumirse baixo o Cuarto teorema do isomorfismo que mostramos a continuación.
Cuarto teorema do isomorfismo
[editar | editar a fonte]Sexa un grupo, e un subgrupo normal de . O homomorfismo da proxección canónica define unha correspondencia bixectiva entre o conxunto de subgrupos de contendo e o conxunto dos (todos) subgrupos de . Baixo esta correspondencia, os subgrupos normais correspóndense con subgrupos normais.
Este teorema denomínanse tamén como o teorema da retícula, teorema de correspondencia.
Comentarios
[editar | editar a fonte]O primeiro teorema do isomorfismo pode ser expresado en teoría das categoría coomo que a categoría de grupos é (epi normal, mono) factorizábel; noutras palabras, os epimorfismos normais e os monomorfismos forman un sistema de factorización para a categoría. Isto está capturado no diagrama conmutativo na marxe, que mostra os obxectos e morfismos cuxa existencia pode deducirse do morfismo . O diagrama mostra que cada morfismo na categoría de grupos ten un kernel no sentido da teoría das categorías; o morfismo arbitrario f factoriza en , onde é un monomorfismo e é un epimorfismo (na categoría conormal, todos os epimorfismos son normais). Isto está representado no diagrama por un obxecto e un monomorfismo (os kernels son sempre monomorfismos), que completan a secuencia exacta curta que vai desde a parte inferior esquerda ata a parte superior dereita do diagrama. O uso da convención da secuencia exacta sálvanos de ter que debuxar os morfismos cero de cara a e cara a .
No segundo teorema do isomorfismo, o produto SN é o join de S e N na rede de subgrupos de G, mentres que a intersección S ∩ N é o meet.
O terceiro teorema do isomorfismo é xeneralizado polo lema nove para categorías abelianas e máis en xeral mapas entre obxectos.
Álxebra Universal
[editar | editar a fonte]Para xeneralizar o visto anteriormente para grupos na álxebra universal, os subgrupos normais deben ser substituídos por relacións de congruencia.
Imos mostra un exemplo para o teorema fundamental do isomorfismo.
Primeiro teorema do isomorfismo na álxebra universal
[editar | editar a fonte]Sexa unha álxebra homomorfismo. Entón a imaxe de é unha subalxebra de , a relación dada por (é dicir, o kernel de ) é unha congruencia sobre , e as álxebras e son isomorfas. (Note que no caso dun grupo, se e só se , así cubrimos a noción de kernel usado na teoría de grupos neste caso.)
Notas
[editar | editar a fonte]Véxase tamén
[editar | editar a fonte]Bibliografía
[editar | editar a fonte]- Noether, Emmy, Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern, Mathematische Annalen 96 (1927) pp. 26–61
- McLarty, Colin, "Emmy Noether's 'Set Theoretic' Topology: From Dedekind to the rise of functors". The Architecture of Modern Mathematics: Essays in history and philosophy (edited by Jeremy Gray e José Ferreirós), Oxford University Press (2006) pp. 211–35.
- Jacobson, Nathan (2009). Basic algebra 1 (2nd ed.). Dover. ISBN 9780486471891.
- Cohn, Paul M., Universal algebra, Chapter II.3 p. 57
- Milne, James S. (2013). Group Theory. 3.13.
- van der Waerden, B. I. (1994). Algebra 1 (9 ed.). Springer-Verlag.
- Dummit, David S.; Foote, Richard M. (2004). Abstract algebra. Hoboken, NJ: Wiley. ISBN 978-0-471-43334-7.
- Burris, Stanley; Sankappanavar, H. P. (2012). A Course in Universal Algebra (PDF). ISBN 978-0-9880552-0-9.
- Scott, W. R. (1964). Group Theory. Prentice Hall.
- Durbin, John R. (2009). Modern Algebra: An Introduction (6 ed.). Wiley. ISBN 978-0-470-38443-5.
- Knapp, Anthony W. (2016). Basic Algebra (Digital second ed.).
- Grillet, Pierre Antoine (2007). Abstract Algebra (2 ed.). Springer.
- Rotman, Joseph J. (2003). Advanced Modern Algebra (2 ed.). Prentice Hall. ISBN 0130878685.
- Hungerford, Thomas W. (1980). Algebra (Graduate Texts in Mathematics, 73). Springer. ISBN 0387905189.
Outros artigos
[editar | editar a fonte]Ligazóns externas
[editar | editar a fonte]






































