Prolongamento analítico

Na análise complexa, unha rama das matemáticas, o prolongamento analítica (ou continuación analítica ou expansión analítica) é unha técnica para estender o dominio de definición dunha función analítica dada. O prolongamento analítico a miúdo consegue definir máis valores dunha función, por exemplo nunha nova rexión onde a representación da serie infinita que inicialmente definiu a función vólvese diverxente.

Discusión inicial

Supoña que f é unha función analítica definida nun subconxunto aberto non baleiro U do plano complexo $\mathbb {C}$ . Se V é un subconxunto aberto maior de $\mathbb {C}$ , que contén U, e F é unha función analítica definida en V tal que

F(z)=f(z)\qquad \forall z\in U,

entón F chámase prolongamento analítico de f. Noutras palabras, a restrición de F en U é a función f coa que comezamos.

Os prolongamentos analíticos son únicos no seguinte sentido: se V é o dominio conexo de dúas funcións analíticas F₁ e F₂ tal que U está contido en V e para todo z en U

F_{1}(z)=F_{2}(z)=f(z),

Unha forma común de definir funcións na análise complexa procede especificando primeiro a función só nun pequeno dominio e, a continuación, estendela mediante o prolongamento analítico.

F_{1}=F_{2}

en todo V. Isto é porque F₁ − F ₂ é unha función analítica que desaparece no dominio aberto e conexo U de f e, polo tanto, debe desaparecer en todo o seu dominio. Isto dedúcese directamente do teorema da identidade para funcións holomorfas.

Aplicacións

Unha forma común de definir funcións na análise complexa procede especificando primeiro a función só nun pequeno dominio e, a continuación, estendela mediante o prolongamento analítico.

Na práctica, este prolongamento adoita facerse estabelecendo primeiro algunha ecuación funcional no pequeno dominio e despois usando esta ecuación para estender o dominio. Exemplos son a función zeta de Riemann e a función gamma.

O concepto de recubrimento universal desenvolveuse por primeira vez para definir un dominio natural para o prolongamento analítico dunha función analítica. A idea de atopar o prolongamento analítico máximo dunha función levou á súa vez ao desenvolvemento da idea das superficies de Riemann.

O prolongamento analítico úsase nas variedades de Riemann, no contexto das solucións das ecuacións de Einstein. Por exemplo, as coordenadas de Schwarzschild pódense prolongar analiticamente nas coordenadas de Kruskal–Szekeres.^[1]

Exemplo detallado

Continuación analítica de U (centrado en 1) a V (centrado en a=(3+i)/2)

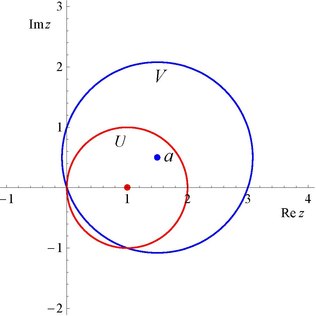
Comezamos cunha función analítica particular $f$ . Neste caso, vén dada por unha serie de potencias centrada en $z=1$ :

f(z)=\sum _{k=0}^{\infty }(-1)^{k}(z-1)^{k}.

Segundo o teorema de Cauchy-Hadamard, o seu raio de converxencia é 1. É dicir, $f$ é definida e analítica no conxunto aberto $U=\{|z-1|<1\}$ que ten fronteira $\partial U=\{|z-1|=1\}$ . De feito, a serie diverxe en $z=0\in \partial U$ .

Facemos como que non sabemos que $f(z)=1/z$ , e pasamos a centrar a serie de potencias nun punto diferente $a\in U$ :

f(z)=\sum _{k=0}^{\infty }a_{k}(z-a)^{k}.

Podemos continuar o proceso: seleccionar $b\in U\cup V$ , recentrar a serie de potencias en $b$ , e determinar onde converxe a nova serie de potencias. Se a rexión contén puntos que non están dentro de $U\cup V$ , entón teremos continuado analiticamente $f$ aínda máis lonxe. Esta $f$ en particular pódese prolongar analiticamente ata todo o plano complexo $\mathbb {C} \setminus \{0\}.$

A distancia dende $a$ a $\partial U$ é $\rho =1-|a-1|>0$ . Tomamos $0<r<\rho$ ; sexa $D$ o disco de raio $r$ arredor de $a$ ; e sexa $\partial D$ a súa fronteira. Entón $D\cup \partial D\subset U$ . Usando a fórmula de diferenciación de Cauchy para calcular os novos coeficientes, temos

{\begin{aligned}a_{k}&={\frac {f^{(k)}(a)}{k!}}\\&={\frac {1}{2\pi i}}\int _{\partial D}{\frac {f(\zeta )d\zeta }{(\zeta -a)^{k+1}}}\\&={\frac {1}{2\pi i}}\int _{\partial D}{\frac {\sum _{n=0}^{\infty }(-1)^{n}(\zeta -1)^{n}d\zeta }{(\zeta -a)^{k+1}}}\\&={\frac {1}{2\pi i}}\sum _{n=0}^{\infty }(-1)^{n}\int _{\partial D}{\frac {(\zeta -1)^{n}d\zeta }{(\zeta -a)^{k+1}}}\\&={\frac {1}{2\pi i}}\sum _{n=0}^{\infty }(-1)^{n}\int _{0}^{2\pi }{\frac {(a+re^{i\theta }-1)^{n}rie^{i\theta }d\theta }{(re^{i\theta })^{k+1}}}\\&={\frac {1}{2\pi }}\sum _{n=0}^{\infty }(-1)^{n}\int _{0}^{2\pi }{\frac {(a-1+re^{i\theta })^{n}d\theta }{(re^{i\theta })^{k}}}\\&={\frac {1}{2\pi }}\sum _{n=0}^{\infty }(-1)^{n}\int _{0}^{2\pi }{\frac {\sum _{m=0}^{n}{\binom {n}{m}}(a-1)^{n-m}(re^{i\theta })^{m}d\theta }{(re^{i\theta })^{k}}}\\&={\frac {1}{2\pi }}\sum _{n=0}^{\infty }(-1)^{n}\sum _{m=0}^{n}{\binom {n}{m}}(a-1)^{n-m}r^{m-k}\int _{0}^{2\pi }e^{i(m-k)\theta }d\theta \\&={\frac {1}{2\pi }}\sum _{n=k}^{\infty }(-1)^{n}{\binom {n}{k}}(a-1)^{n-k}\int _{0}^{2\pi }d\theta \\&=\sum _{n=k}^{\infty }(-1)^{n}{\binom {n}{k}}(a-1)^{n-k}\\&=(-1)^{k}\sum _{m=0}^{\infty }{\binom {m+k}{k}}(1-a)^{m}\\&=(-1)^{k}a^{-k-1}\end{aligned}}.

A última suma resulta da derivación $k$ -ésima da serie xeométrica, que dá a fórmula

{\frac {1}{(1-x)^{k+1}}}=\sum _{m=0}^{\infty }{\binom {m+k}{k}}x^{m}.

Entón,

{\begin{aligned}f(z)&=\sum _{k=0}^{\infty }a_{k}(z-a)^{k}\\&=\sum _{k=0}^{\infty }(-1)^{k}a^{-k-1}(z-a)^{k}\\&={\frac {1}{a}}\sum _{k=0}^{\infty }\left(1-{\frac {z}{a}}\right)^{k}\\&={\frac {1}{a}}{\frac {1}{1-\left(1-{\frac {z}{a}}\right)}}\\&={\frac {1}{z}}\\&={\frac {1}{(z+a)-a}}\end{aligned}}

que ten raio de converxencia $|a|$ arredor de $0$ . Se escollemos $a\in U$ con $|a|>1$ , entón $V$ non é un subconxunto de $U$ e en realidade é maior en superficie que $U$ . A gráfica mostra o resultado para $a={\tfrac {1}{2}}(3+i).$

Podemos continuar o proceso: seleccionar $b\in U\cup V$ , recentrar a serie de potencias en $b$ , e determinar onde converxe a nova serie de potencias. Se a rexión contén puntos que non están dentro de $U\cup V$ , entón teremos continuado analiticamente $f$ aínda máis lonxe. Esta $f$ en particular pódese continuar analiticamente ata todo o plano complexo $\mathbb {C} \setminus \{0\}.$

Neste caso particular os valores obtidos de $f(-1)$ son iguais cando os centros sucesivos teñen unha parte imaxinaria positiva ou unha parte imaxinaria negativa. Non sempre é así; en particular, este non é o caso do logaritmo complexo, a antiderivada da función anterior.

Definición formal de xerme

A serie de potencias definida a continuación xeneralízase pola idea dun xerme. A teoría xeral do prolongamento analítico e as súas xeneralizacións coñécese como teoría dos feixes. Sexa

f(z)=\sum _{k=0}^{\infty }\alpha _{k}(z-z_{0})^{k}

unha serie de potencias que converxen no disco D_r(z₀), r > 0, definido por

D_{r}(z_{0})=\{z\in \mathbb {C} :|z-z_{0}|<r\}

.

Dicimos que o vector

g=(z_{0},\alpha _{0},\alpha _{1},\alpha _{2},\ldots )

é un xerme de f. A base g₀ de g é z₀, o tronco de g é (α₀, α₁, α₂, ...) e o tope g₁ de g é α₀. O tope de g é o valor de f en z₀.

Calquera vector g = (z₀, α₀, α₁, ...) é un xerme se representa unha serie de potencias dunha función analítica arredor de z₀ con algún raio de converxencia r > 0. Polo tanto, podemos falar con seguridade do conxunto de xermes ${\mathcal {G}}$ .

Exemplo de xerme

L(z)=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}}{k}}(z-1)^{k}

é unha serie de potencias correspondente ao logaritmo natural próximo a z = 1. Esta serie de potencias pódese converter nun xerme

g=\left(1,0,1,-{\frac {1}{2}},{\frac {1}{3}},-{\frac {1}{4}},{\frac {1}{5}},-{\frac {1}{6}},\ldots \right)

Este xerme ten un radio de converxencia de 1, polo que lle corresponde un feixe S. Esta é o faixe da función logaritmo.

Fronteira natural

Supoña que unha serie de potencias ten un raio de converxencia r e define unha función analítica f dentro dese disco. Considere os puntos da circunferencia de converxencia. Un punto para o que hai unha veciñanza no que f ten unha extensión analítica é regular, senón a ten é singular. A circunferencia é un fronteira natural se todos os seus puntos son singulares.

De forma máis xeral, podemos aplicar a definición a calquera dominio conexo aberto no que f sexa analítica e clasificar os puntos da fronteira do dominio como regulares ou singulares: a fronteira do dominio é logo unha fronteira natural se todos os puntos son singulares, nese caso o dominio é un dominio de holomorfia.

Teorema de monodromía

O teorema de monodromía dá unha condición suficiente para a existencia dunha continuación analítica directa (é dicir, unha extensión dunha función analítica a unha función analítica nun conxunto maior).

Supoñamos que $D\subset \mathbb {C}$ é un conxunto aberto e f unha función analítica en D. Se G é un dominio simplemente conexo que contén D, tal que f ten unha continuación analítica ao longo de cada camiño en G, comezando desde algún punto fixo a en D, entón f ten unha continuación analítica directa a G. .

Teorema do oco de Hadamard

Artigo principal: Teorema do oco de Ostrowski-Hadamard.

Para unha serie de potencias

f(z)=\sum _{k=0}^{\infty }a_{k}z^{n_{k}}

con

\liminf _{k\to \infty }{\frac {n_{k+1}}{n_{k}}}>1

a circunferencia de converxencia é unha fronteira natural. Tal serie de potencias chámase lagoa (función analítica que non se pode continuar analiticamente en ningún lugar fóra do raio de converxencia dentro do cal está definida por unha serie de potencias). Este teorema foi substancialmente xeneralizado por Eugen Fabry (ver o teorema do oco de Fabry) e George Pólya.

Teorema de Polya

Sexa

f(z)=\sum _{k=0}^{\infty }\alpha _{k}(z-z_{0})^{k}

unha serie de potencias, entón existe ε_k ∈ {−1, 1} tal que

f(z)=\sum _{k=0}^{\infty }\varepsilon _{k}\alpha _{k}(z-z_{0})^{k}

ten o disco de converxencia de f arredor de z₀ como fronteira natural.

A demostración deste teorema fai uso do teorema do oco de Hadamard.

Notas

↑ Kruskal, M. D. (1960-09-01). "Maximal Extension of Schwarzschild Metric". Physical Review 119 (5): 1743–1745. Bibcode:1960PhRv..119.1743K. doi:10.1103/PhysRev.119.1743.

Véxase tamén

Bibliografía

Lars Ahlfors (1979). Complex Analysis (3 ed.). McGraw-Hill. pp. 172, 284.
Ludwig Bieberbach (1955). Analytische Fortsetzung. Springer-Verlag.
P. Dienes (1957). The Taylor series: an introduction to the theory of functions of a complex variable. New York: Dover Publications, Inc.

Outros artigos

Ligazóns externas

"Analytic continuation". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
Analytic Continuation at MathPages
Weisstein, Eric W. "Analytic Continuation". MathWorld.

[1] Kruskal, M. D. (1960-09-01). "Maximal Extension of Schwarzschild Metric". Physical Review 119 (5): 1743–1745. Bibcode:1960PhRv..119.1743K. doi:10.1103/PhysRev.119.1743.

[1]