Diagrama de Venn

Os diagramas de Venn son esquemas usados na teoría de conxuntos, teoría usada en matemáticas, lóxica de clases e outras disciplinas. Estes diagramas mostran coleccións (conxuntos) de cousas (elementos) por medio circunferencias e un rectángulo global representando o conxunto universal U.

Introdución

Cos diagramas de Venn é posíbel representar as relacións de intersección, inclusión e disxunción sen mudar a posición relativa dos conxuntos

Intersección

Os elementos do conxunto que pertencen simultaneamente a ambos os conxuntos forman a intersección do conxunto.^[1] No diagrama de Venn será a zona delimitada polo cruzamento das dúas circunferencias.

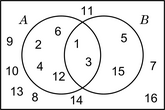
A = {1; 2; 3; 4; 6; 12}
B = {1; 3; 5; 15}
U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16}

Intersección = 1, 3.

Inclusión

Se todos os elementos dun conxunto son parte dos elementos doutro, dise que o primeiro é un subconjunto do segundo ou que está incluído no segundo.^[1]

A = {1; 2; 3; 4; 6; 12}
B = {1; 2; 3; 6}
U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}

Disxunción

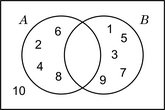
Cando os conxuntos non teñen elementos comúns, a rexión de superposición fica baleira.

A = {2; 4; 6; 8}
B = {1; 3; 5; 7; 9}
U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}

Orixes e historia

Vitral do comedor do Caius College (Cambridge) en homenaxe a John Venn e a súa creación

Os diagramas de Venn teñen o nome do seu creador, John Venn, matemático e filósofo británico.^[2] Estudante e máis tarde profesor do Caius College da Universidade de Cambridge, Venn desenvolveu toda a súa produción intelectual nese ámbito.^[3]

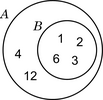
Foi o matemático suízo Leonhard Euler quen primeiro introduciu unha notación clara e sinxela similar aos diagramas de Venn.^[4] O seguinte diagrama mostra doutro xeito a relación de inclusión do exemplo dado na introdución.

diagrama de Euler

Os diagramas de Euler distínguense dos de Venn en dous aspectos:

Neles non aparecen as rexións baleiras
O conxunto universal non se representa.

A primeira constancia escrita do uso da expresión «diagrama de Venn» é moi tardía (1918) e atópase no libro A Survey of Symbolic Logic de Clarence Irving Lewis.^[5]

Diagramas de Venn de enunciados

Podemos ter dous tipos de diagramas de Venn: os que mostran elementos e os que simplemente mostran enunciados ou conceptos. Estes últimos son máis interesantes porque permiten operar de maneira abstracta e chegar a conclusións máis xerais.^[6]

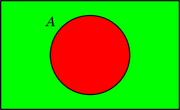
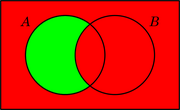
Os seguintes diagramas do segundo tipo mostran os resultados de catro operacións básicas con conxuntos usando o código do semáforo de dúas cores.^[7]


¬A	A ∧ B	A ∨ B = ¬((¬A) ∧ (¬B))	A – B = A ∧ (¬B)

Que representan as operacións: negación, conxunción, disxunción e diferenza. En verde están o resultado das operacións.

Outras representacións

Diagramas de Euler

Artigo principal: Diagrama de Euler.

Os diagramas de Euler preceden historicamente aos diagramas de Venn e nalgunhas aplicacións son aínda usados.

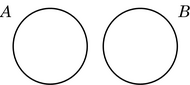
A diferenza entre os diagramas de Euler e de Venn obsérvase sobre todo nas relacións de inclusión e de disxunción.

	inclusión	disxunción
Euler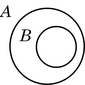
Venn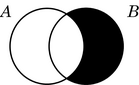

Mapas de Karnaugh

Artigo principal: Mapa de Karnaugh.

Os mapas de Karnaugh ou diagramas de Veitch son unha representación visual de expresións da álxebra de Boole.^[8]

Notas

↑ ^1,0 ^1,1 Luetich, "Ser o ser no, ése es el dilema", Actas – Suplemento 1, 1 (1) 1, Rosario, Academia Luventicus, 2001
↑ Margaret E. Baron, "A Note on the Historical Development of Logic Diagrams: Leibniz, Euler and Venn", The Mathematical Gazette, Vol. 53 No. 384, Leicester, The Mathematical Association, 1969
↑ Anónimo, "Obituary Notices of Fellows Deceased: Rudolph Messel, Frederick Thomas Trouton, John Venn, John Young Buchanan, Oliver Heaviside, Andrew Gray", Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, Vol. 110 No. 756, Londres, The Royal Society, 1926
↑ Edward N. Zalta – Uri Nodelman – Colin Allen (editores), "Diagrams", Stanford Encyclopedia of Philosophy, Stanford, Metaphysics Research Lab – Center for the Study of Language and Information – Stanford University, 2001–2013
↑ John Venn, The Principles Of Empirical Or Inductive Logic, Londres, Macmillan, 1907
↑ Juan José Luetich, "Ser y pertenecer", Actas – Suplemento 1, 1 (2) 1, Rosario, Academia Luventicus, 2008
↑ Javier R. Movellan, "Tutorial on axiomatic ser theory" Arquivado 05 de agosto de 2012 en Wayback Machine., Tutorial on axiomatic ser theory, Kolmogorov Project, 2003
↑ Andreas Otte, "Venn-Diagramme: Einleitung", Begriffslogik.de, 1998

Véxase tamén

Outros artigos

Ligazóns externas

plantillaarbolgenealogico.net/diagramas/venn/ : Conceptos e exemplos relacionados co diagrama de Venn.
Winvenn Arquivado 21 de marzo de 2020 en Wayback Machine.: Programa para explorar a notación da teoría de conxuntos sombreando diagramas.
XFig: Programa de creación de gráficos con licenza GPL.
Diagrama de Venn: Qué es, para qué se utiliza y cómo hacerlo. (en castelán)

[Luetich1-1] 1,0 ^1,1 Luetich, "Ser o ser no, ése es el dilema", Actas – Suplemento 1, 1 (1) 1, Rosario, Academia Luventicus, 2001

[MB-2] Margaret E. Baron, "A Note on the Historical Development of Logic Diagrams: Leibniz, Euler and Venn", The Mathematical Gazette, Vol. 53 No. 384, Leicester, The Mathematical Association, 1969

[3] Anónimo, "Obituary Notices of Fellows Deceased: Rudolph Messel, Frederick Thomas Trouton, John Venn, John Young Buchanan, Oliver Heaviside, Andrew Gray", Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, Vol. 110 No. 756, Londres, The Royal Society, 1926

[ZNA-4] Edward N. Zalta – Uri Nodelman – Colin Allen (editores), "Diagrams", Stanford Encyclopedia of Philosophy, Stanford, Metaphysics Research Lab – Center for the Study of Language and Information – Stanford University, 2001–2013

[5] John Venn, The Principles Of Empirical Or Inductive Logic, Londres, Macmillan, 1907

[6] Juan José Luetich, "Ser y pertenecer", Actas – Suplemento 1, 1 (2) 1, Rosario, Academia Luventicus, 2008

[7] Javier R. Movellan, "Tutorial on axiomatic ser theory" Arquivado 05 de agosto de 2012 en Wayback Machine., Tutorial on axiomatic ser theory, Kolmogorov Project, 2003

[8] Andreas Otte, "Venn-Diagramme: Einleitung", Begriffslogik.de, 1998

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]