Grafo

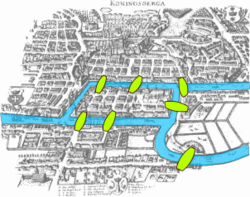
En matemáticas e ciencias da computación, un grafo^[1] (do grego grafos: debuxo, imaxe) ou gráfica é o principal obxecto de estudo da teoría de grafos. Informalmente, un grafo é un conxunto de obxectos chamados vértices ou nós unidos por enlaces chamados arestas ou arcos, que permiten representar relacións binarias entre elementos dun conxunto.

Definicións

As definicións na teoría de grafos varían. As seguintes son algunhas das formas máis básicas de definir grafos e as estruturas matemáticas relacionadas.

Grafo

Un grafo (ás veces chamado grafo non orientado ou grafo non dirixido para distinguilo dun grafo orientado, ou tamén chamado grafo simple cando se quere distinguir dun multigrafo)^[2] é un par $G = (V, E)$ , onde $V$ é un conxunto cuxos elementos se chaman vértices, e $E$ é un conxunto de pares non ordenados de vértices $\{v_{1},v_{2}\}$ , cuxos elementos se denominan arestas (ás veces ligazóns ou liñas).

Grafo orientado

Artigo principal: Grafo orientado.

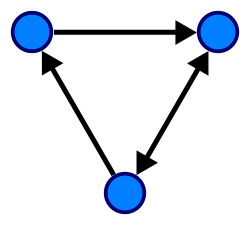
Un grafo orientado ou grafo dirixido ou digrafo é un grafo no que as arestas teñen orientacións.

Nun sentido restrinxido pero moi común do termo,^[3] un grafo orientado é un par $G = (V, E)$ que comprende:

$V$ , un conxunto de vértices (tamén chamados nós ou puntos);
$E$ , un conxunto de arestas (tamén chamadas arestas orientadas, ligazóns orientadas, liñas orientadas, frechas ou arcos), que son pares ordenados de vértices distintos $E\subseteq \{(x,y)\mid (x,y)\in V^{2}\;{\textrm {and}}\;x\neq y\}$ .

Gráfico mixto

Artigo principal: Grafo mixto.

Un grafo mixto é un grafo no que algunhas arestas poden estar orientadas e outras non.

Grafo ponderado

Un grafo ponderado ou unha rede ponderada^[4]^[5] é un grafo no que se lle asigna un número (o peso) a cada aresta.^[6]

Eses pesos poden representar, por exemplo, custos, lonxitudes ou capacidades, dependendo do problema que se trate. Estes grafos xorden en moitos contextos, por exemplo no problema do camiño máis curto como o problema do viaxeiro.

Tipos de grafos

Grsfo orientado simple

Unha definición de grafo orientado simple é a dun grafo orientado no que como máximo un de (x, y) e (y, x) poden ser arestas do grafo.

Algúns autores usan definicións con algunha pequena variante.

Grafo regular

Artigo principal: Grafo regular.

Un grafo regular é un grafo no que cada vértice ten o mesmo número de veciños, é dicir, cada vértice ten o mesmo grao. Un grafo regular con vértices de grao k chámase grafo k regular ou grafo regular de grao k.

Grafo completo

Artigo principal: Grafo completo.

Un grafo completo é un grafo no que cada par de vértices está unido por unha aresta. Un grafo completo contén todas as arestas posíbeis.

Grafo finito

Un grafo finito é un grafo no que o conxunto de vértices e o conxunto de arestas son conxuntos finitos. No caso contrario, chámase grafo infinito.

O máis común na teoría de grafos dáse a entender que os grafos discutidos son finitos.

Grafo conexo

Artigo principal: Conectividade (teoría de grafos).

Nun grafo non orientado, un par non ordenado de vértices {x, y} chámase conectado se un camiño leva de x a y. En caso contrario, o par non ordenado chámase non conectado.

Un grafo conexo é un grafo non orientado no que cada par de vértices non ordenados do grafo está conectado. En caso contrario, chámase grafo non conexo.

Grafo bipartito

Artigo principal: Grafo bipartito.

Un grafo bipartito é un grafo sinxelo no que o conxunto de vértices pode ser particionado en dous conxuntos, W e X, de xeito que non hai dous vértices en W que compartan unha aresta común nin dous vértices en X compartan unha aresta común. Alternativamente, é un grafo cun número cromático de 2.

Nun grafo bipartito completo, o conxunto de vértices é a unión de dous conxuntos disxuntos, W e X, de xeito que cada vértice en W é adxacente a cada vértice en X pero non hai arestas dentro de W ou X.

Grafo camiño

Artigo principal: Gráfico camiño.

Un grafo camiño ou grafo linear de orde n ≥ 2 é un grafo no que os vértices poden ser listados nunha orde v₁, v₂, …, v_n tal que as arestas son os {v_i, v_i+1} onde i = 1, 2, ..., n − 1. Os grafos camiño pódense caracterizar como grafos conexos nos que o grao de todos os vértices é 2 agás dous vértices de grao 1.

Grafo plano

Artigo principal: Grafo plano.

Un grafo plano é un grafo cuxos vértices e arestas se poden debuxar nun plano de forma que non se corten dúas das arestas.

Grafo cíclico

Artigo principal: Grafo cíclico.

Un grafo cíclico ou grafo circular de orde n ≥ 3 é un grafo no que os vértices poden ser listados nunha orde v₁, v₂, …, v_n tal que as arestas son os {v_i, v_i+1} onde i = 1, 2, …, n − 1, máis a última aresta fechando o ciclo {v_n, v₁}. Os grafos cíclicos pódense caracterizar como grafos conexos nos que o grao de todos os vértices é 2. Se un grafo cíclico aparece como un subgrafo doutro grafo daquela é un ciclo ou circuíto nese grafo.

Árbore

Artigo principal: Árbore (teoría de grafos).

Unha árbore é un grafo non orientado no que dous vértices están conectados por exactamente un camiño, ou equivalentemente é un grafo conexo acíclico non orientado.

Poliárbore

Artigo principal: Poliárbore.

Unha poliárbore (ou árbore orientada ou rede únicamente conexa) é un grafo acíclico orientado (DAG, polas súas siglas en inglés) cuxo grafo non orientado subxacente é unha árbore.

Características

Tipicamente, un grafo represéntase graficamente como un conxunto de puntos (vértices ou nós) unidos por liñas (arestas).

Dende un punto de vista práctico, os grafos permiten estudar as interrelacións entre unidades que interactúan as unhas coas outras. Por exemplo, unha rede de computadoras pódese representar e estudar mediante un grafo, no que os vértices representan terminais e as arestas representan conexións (que á súa vez, poden ser cables ou conexións inalámbricas).

Practicamente calquera problema pode ser representado mediante un grafo, e o seu estudo transcende a diversas áreas das ciencias exactas e das ciencias sociais.

Exemplos

Un grafo con seis vértices e sete arestas

O diagrama da dereita é unha representación esquemática do grafo con vértices $V=\{1,2,3,4,5,6\}$ e arestas $E=\{\{1,2\},\{1,5\},\{2,3\},\{2,5\},\{3,4\},\{4,5\},\{4,6\}\}.$
En ciencias da computación, os grafos orientados utilízanse para representar coñecemento (por exemplo, máquinas de estados finitos e moitas outras estruturas discretas.
Unha relación binaria R nun conxunto X define un grafo orientado. Un elemento x de X é un predecesor directo dun elemento y de X se e só se xRy.

Notas

↑ Definicións no Dicionario da Real Academia Galega e no Portal das Palabras para grafo.
↑ Bender & Williamson 2010, p. 148.
↑ Bender & Williamson 2010, p. 161.
↑ Strang, Gilbert (2005). Linear Algebra and Its Applications (4th ed.). Brooks Cole. ISBN 978-0-03-010567-8.
↑ Lewis, John (2013). Java Software Structures (4th ed.). Pearson. p. 405. ISBN 978-0133250121.
↑ Fletcher, Peter; Hoyle, Hughes; Patty, C. Wayne (1991). Foundations of Discrete Mathematics (International student ed.). Boston: PWS-KENT Pub. Co. pp. 463. ISBN 978-0-53492-373-0.

Véxase tamén

Bibliografía

Trudeau, Richard J. (1993). Introduction to Graph Theory (Corrected, enlarged republication. ed.). Nova York: Dover Publications. ISBN 978-0-486-67870-2. Consultado o 8-8-2012.

Ligazóns externas

Graph en MathWorld

[1] Definicións no Dicionario da Real Academia Galega e no Portal das Palabras para grafo.

[FOOTNOTEBenderWilliamson2010148-2] Bender & Williamson 2010, p. 148.

[FOOTNOTEBenderWilliamson2010161-3] Bender & Williamson 2010, p. 161.

[4] Strang, Gilbert (2005). Linear Algebra and Its Applications (4th ed.). Brooks Cole. ISBN 978-0-03-010567-8.

[5] Lewis, John (2013). Java Software Structures (4th ed.). Pearson. p. 405. ISBN 978-0133250121.

[6] Fletcher, Peter; Hoyle, Hughes; Patty, C. Wayne (1991). Foundations of Discrete Mathematics (International student ed.). Boston: PWS-KENT Pub. Co. pp. 463. ISBN 978-0-53492-373-0.

[1]

[2]

[3]

[4]

[5]

[6]