Modelo:Bloque numerado

[ máis información | ver o historial | | | ver as instrucións ]

Indicacións de uso do modelo

Este modelo crea un bloque numerado que xeralmente se usa para numerar fórmulas matemáticas. Este modelo pode usarse xunto con {{EquationRef}} e {{EquationNote}} para producir ecuacións numeradas cun formato elegante se se quere facer unha referencia a unha ecuación.

Parámetros

Comando: {{NumBlk|<1>|<2>|<3>|RawN=<>|LnSty=<>|Border=<>}}

Requírense os parámetros {{{1}}}, {{{2}}}, e {{{3}}} deste modelo. Ademais, hai tres parámetros opcionais {{{RawN}}}, {{{LnSty}}} e {{{Border}}}.

{{{1}}}: Especificar indentación (a ecuación empeza máis á dereita con sangría). Cantos máis signos de dous puntos (:) poña, máis indentado estará o bloque, ata un límite de 20. Este parámetro pode estar baleiro se non é necesaria unha indentación.

{{{2}}}: O corpo ou contido do bloque.

{{{3}}}: Especificar o número do bloque.

{{{RawN}}}: Se un valor non baleiro ou non de espazo en branco, non se aplicará ningún formato extra ao bloque numérico.

{{{LnSty}}}: Especificar o estilo de liña.

{{{Border}}}: Se se establece, pon unha caixa arredor da ecuación. (Experimental.)

Exemplos

As ecuacións poden render HTML
{{NumBlk|:|<math>y=ax+b</math>|Eq. 3}}	$y=ax+b$         (Ec. 3)
{{NumBlk|:|<math>ax^2+bx+c=0</math>|Ec. 3}}	$ax^{2}+bx+c=0$         (Ec. 3)
{{NumBlk|:|<math>\Psi(x_1,x_2)=U(x_1)V(x_2)</math>|2}}	$\Psi (x_{1},x_{2})=U(x_{1})V(x_{2})$         (2)
Indentación
{{NumBlk||<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3.5}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         (3.5)
{{NumBlk|:|<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|1}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         (1)
{{NumBlk|::|<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|13.7}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         (13.7)
{{NumBlk|:::|<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|1.2}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         (1.2)
Formato do número da ecuación
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=3.5|RawN=.}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         3.5
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=<3.5>|RawN=.}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         <3.5>
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=[3.5]|RawN=.}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         [3.5]
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3='''[3.5]'''|RawN=.}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         [3.5]
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=<Big>'''[3.5]'''</Big>}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         ([3.5])
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=<Big>'''[3.5]'''</Big>|RawN=.}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         [3.5]
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=<math>(3.5)</math>|RawN=.}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         $(3.5)\,$
Estilo de liña
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=<Big>'''(3.5)'''</Big>|RawN=.|LnSty=1px dashed red}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         (3.5)
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=<Big>'''(3.5)'''</Big>|RawN=.|LnSty=3px dashed #0a7392}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         (3.5)
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=<Big>'''[3.5]'''</Big>|RawN=.|LnSty=3px solid green}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         [3.5]
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=<Big>'''[3.5]'''</Big>|RawN=.|LnSty=5px dotted blue}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         [3.5]
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=<Big>'''[3.5]'''</Big>|RawN=.|LnSty=0px solid green}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         [3.5]
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=<Big>'''[3.5]'''</Big>|RawN=.|LnSty=5px none green}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         [3.5]
{{NumBlk|1=:|2=<math>\mathbf{a}(t)=\frac{d}{dt}\mathbf{v}(t)</math>|3=<Big>'''[3.5]'''</Big>|RawN=.|LnSty=3px double green}}	$\mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)$         [3.5]
Altura de liña e indentación (1)
As seguintes ecuacións :<math>3x+2y-z=1</math> :<math>2x-2y+4z=-2</math> :<math>-2x+y-2z=0</math> forman un sistema de tres ecuacións.	As seguintes ecuacións $3x+2y-z=1$ $2x-2y+4z=-2$ $-2x+y-2z=0$ forman un sistema de tres ecuacións.
As seguintes ecuacións {{NumBlk|:|<math>3x+2y-z=1</math>|1}} {{NumBlk|:|<math>2x-2y+4z=-2</math>|2}} {{NumBlk|:|<math>-2x+y-2z=0</math>|3}} forman un sistema de tres ecuacións.	As seguintes ecuacións $3x+2y-z=1$         (1) $2x-2y+4z=-2$         (2) $-2x+y-2z=0$         (3) forman un sistema de tres ecuacións.
As seguintes ecuacións <div style="line-height: 0.7105;"> {{NumBlk|:|<math>3x+2y-z=1</math>|1}} {{NumBlk|:|<math>2x-2y+4z=-2</math>|2}} {{NumBlk|:|<math>-2x+y-2z=0</math>|3}} </div> forman un sistema de tres ecuacións.	As seguintes ecuacións $3x+2y-z=1$         (1) $2x-2y+4z=-2$         (2) $-2x+y-2z=0$         (3) forman un sistema de tres ecuacións.
As seguintes ecuacións <div style="line-height: 0.7105;"> {{NumBlk||<math>3x+2y-z=1</math>|1}} {{NumBlk||<math>2x-2y+4z=-2</math>|2}} {{NumBlk||<math>-2x+y-2z=0</math>|3}} </div> forman un sitema de tres ecuacións.	As seguintes ecuacións $3x+2y-z=1$         (1) $2x-2y+4z=-2$         (2) $-2x+y-2z=0$         (3) forman un sistema de tres ecuacións.
As seguintes ecuacións <div style="line-height: 0.7105; margin-left: 1.6em;"> {{NumBlk||<math>3x+2y-z=1</math>|1}} {{NumBlk||<math>2x-2y+4z=-2</math>|2}} {{NumBlk||<math>-2x+y-2z=0</math>|3}} </div> forman un sistema de tres ecuacións.	As seguintes ecuacións $3x+2y-z=1$         (1) $2x-2y+4z=-2$         (2) $-2x+y-2z=0$         (3) forman un sistema de tres ecuacións.
Altura de liña e indentación (2)
As seguintes ecuacións :<math>3x+2y-z=1</math> ::<math>2x-2y+4z=-2</math> :::<math>-2x+y-2z=0</math> forman un sistrema de tres ecuacións.	As seguintes ecuacións $3x+2y-z=1$ $2x-2y+4z=-2$ $-2x+y-2z=0$ forman un sistema de tres ecuacións.
As seguintes ecuacións <div style="line-height: 0.7105; margin-left: 1.6em;"> {{NumBlk||<math>3x+2y-z=1</math>|1}} <div style="margin-left: 1.6em;"> {{NumBlk||<math>2x-2y+4z=-2</math>|2}} <div style="margin-left: 1.6em;"> {{NumBlk||<math>-2x+y-2z=0</math>|3}} </div> </div> </div> forman un sistema de tres ecuacións.	As seguin tes ecuacións $3x+2y-z=1$         (1) $2x-2y+4z=-2$         (2) $-2x+y-2z=0$         (3) forman un sitema de tres ecuacións.
As seguintes ecuacións <div style="line-height: 0.7105;"> <div style="margin-left: calc(1.6em * 1);"> {{NumBlk||<math>3x+2y-z=1</math>|1}} </div> <div style="margin-left: calc(1.6em * 2);"> {{NumBlk||<math>2x-2y+4z=-2</math>|2}} </div> <div style="margin-left: calc(1.6em * 3);"> {{NumBlk||<math>-2x+y-2z=0</math>|3}} </div> </div> forman un sistema de tres ecuacións.	As seguintes ecuacións $3x+2y-z=1$         (1) $2x-2y+4z=-2$         (2) $-2x+y-2z=0$         (3) forman un sistema de tres ecuacións.
Lista non ordenada
* <math>3x+2y-z=1</math> * <math>2x-2y+4z=-2</math> * <math>-2x+y-2z=0</math>	$3x+2y-z=1$ $2x-2y+4z=-2$ $-2x+y-2z=0$
* {{NumBlk||<math>3x+2y-z=1</math>|Ec. 1}} * {{NumBlk||<math>2x-2y+4z=-2</math>|Ec. 2}} * {{NumBlk||<math>-2x+y-2z=0</math>|Ec. 3}}	$3x+2y-z=1$         (Ec. 1) $2x-2y+4z=-2$         (Ec. 2) $-2x+y-2z=0$         (Ec. 3)
<ul style="line-height: 0.7105;"> <li><div style="display: inline-block; width: 100%; vertical-align: middle;">{{NumBlk||<math>3x+2y-z=1</math>|Ec. 1}}</div></li> <li><div style="display: inline-block; width: 100%; vertical-align: middle;">{{NumBlk||<math>2x-2y+4z=-2</math>|Ec. 2}}</div></li> <li><div style="display: inline-block; width: 100%; vertical-align: middle;">{{NumBlk||<math>-2x+y-2z=0</math>|Ec. 3}}</div></li> </ul>	$3x+2y-z=1$         (Ec. 1) $2x-2y+4z=-2$         (Ec. 2) $-2x+y-2z=0$         (Ec. 3)
<ul style="line-height: 0.7105;"> <li><div style="display: inline-table; width: 100%; vertical-align: middle;">{{NumBlk||<math>3x+2y-z=1</math>|Ec. 1}}</div></li> <li><div style="display: inline-table; width: 100%; vertical-align: middle;">{{NumBlk||<math>2x-2y+4z=-2</math>|Ec. 2}}</div></li> <li><div style="display: inline-table; width: 100%; vertical-align: middle;">{{NumBlk||<math>-2x+y-2z=0</math>|Ec. 3}}</div></li> </ul>	$3x+2y-z=1$         (Ec. 1) $2x-2y+4z=-2$         (Ec. 2) $-2x+y-2z=0$         (Ec. 3)
Lista ordenada
# <math>3x+2y-z=1</math> # <math>2x-2y+4z=-2</math> # <math>-2x+y-2z=0</math>	$3x+2y-z=1$ $2x-2y+4z=-2$ $-2x+y-2z=0$
# {{NumBlk||<math>3x+2y-z=1</math>|Ec. 1}} # {{NumBlk||<math>2x-2y+4z=-2</math>|Ec. 2}} # {{NumBlk||<math>-2x+y-2z=0</math>|Ec. 3}}	$3x+2y-z=1$         (Ec. 1) $2x-2y+4z=-2$         (Ec. 2) $-2x+y-2z=0$         (Ec. 3)
<ol style="line-height: 0.7105;"> <li><div style="display: inline-block; width: 100%; vertical-align: middle;">{{NumBlk||<math>3x+2y-z=1</math>|Ec. 1}}</div></li> <li><div style="display: inline-block; width: 100%; vertical-align: middle;">{{NumBlk||<math>2x-2y+4z=-2</math>|Ec. 2}}</div></li> <li><div style="display: inline-block; width: 100%; vertical-align: middle;">{{NumBlk||<math>-2x+y-2z=0</math>|Ec. 3}}</div></li> </ol>	$3x+2y-z=1$         (Ec. 1) $2x-2y+4z=-2$         (Ec. 2) $-2x+y-2z=0$         (Ec. 3)
<ol style="line-height: 0.7105;"> <li><div style="display: inline-table; width: 100%; vertical-align: middle;">{{NumBlk||<math>3x+2y-z=1</math>|Ec. 1}}</div></li> <li><div style="display: inline-table; width: 100%; vertical-align: middle;">{{NumBlk||<math>2x-2y+4z=-2</math>|Ec. 2}}</div></li> <li><div style="display: inline-table; width: 100%; vertical-align: middle;">{{NumBlk||<math>-2x+y-2z=0</math>|Ec. 3}}</div></li> </ol>	$3x+2y-z=1$         (Ec. 1) $2x-2y+4z=-2$         (Ec. 2) $-2x+y-2z=0$         (Ec. 3)
Bordo
{{NumBlk|:|<math>y=ax+b</math>|Ec. 3|Border=1}}	$y=ax+b$         (Ec. 3)

Posición relativa a imaxes que a rodean

Os bloques numerados deberían poder situarse arredor de imaxes que ocupan espazo á esquerda ou dereita da pantalla. Para asegurar que o bloque numerado ten acceso a toda a liña, considere usar un modelo de tipo {{clear}}.

Para ilustar isto, considere este exemplo:

Markup

[[Ficheiro:Bnet_fan2.png|miniatura|dereita|Fig.1: Representación de rede bayasiana de Ec.(6)]] [[Ficheiro:Bnet_fan2.png|miniatura|esquerda|Fig.1: Representación de rede bayesiana de Ec.(6)]] <br><br>Unha rede bayesiana (ou rede de crenza) é un modelo gráfico probabilístico que representa un conxunto de variables e as súas independencias probabilísticas. Por exemplo, unha rede bayesiana poder´`ia representar as relacións probabilísticas entre enfermidades e síntomas. Ddos os síntomas, a rede pode usarse para computar as probablilidades da presenza de varias enfermidades. {{NumBlk|1=:|2=<math> P(a, b, \lambda) = P(a| \lambda) P(b | \lambda) P(\lambda)\, </math>,|3='''Ec.(6)'''|RawN=.}}

Dá lugar a

Fig.1: Representación de rede bayesiana de Ec.(6) Fig.1: Representación de rede bayesiana de Ec.(6) Unha rede bayesiana (ou rede de crenza) é un modelo gráfico probabilístico que representa un conxunto de variables e as súas independencias probabilísticas. Por exemplo, unha rede bayesiana poderia representar as relacións probabilísticas entre enfermidades e síntomas. Dados os síntomas, a rede pode usarse para computar as probabilidades da presenza de varias enfermidades. $P(a,b,\lambda )=P(a|\lambda )P(b|\lambda )P(\lambda )\,$,         Ec.(6)

Se se desexa que un bloque numerado se extenda por toda a liña, debería sitarse un modelo {{clear}} diante del.

Markup

[[Ficheiro:Bnet_fan2.png|miniatura|dereita|Fig.1: Representación de rede bayesiana de Ec.(6)]] [[Ficheiro:Bnet_fan2.png|miniatura|esquerda|Fig.1: Representación de rede bayesiana de Ec.(6)]] <br><br>Unha rede bayesiana (ou rede de crenza) é un modelo gráfico probabilístico que representa un conxunto de variables e as súas independencias probabilísticas. Por exemplo, unha rede bayesiana poderia representar as relacións probabilísticas entre enfermidades e síntomas. Dados os síntomas, a rede pode usarse para computar as probabilidades da presenza de varias enfermidades. {{clear}} {{NumBlk|1=:|2=<math> P(a, b, \lambda) = P(a| \lambda) P(b | \lambda) P(\lambda)\, </math>,|3='''Eq.(6)'''|RawN=.}}

Dá lugar a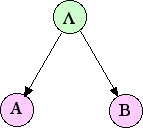

Fig.1: Representación de rede bayesiana de Ec.(6) Fig.1: Represenación de rede bayesiaa de Ec.(6) Unha rede bayesiana (ou rede de crenza) é un modelo gráfico probabilístico que representa un conxunto de variables e as súas independencias probabilísticas. Por exemplo, unha rede bayesiana poderia representar as relacións probabilísticas entre enfermidades e síntomas. Dados os síntomas, a rede pode usarse para computar as probabilidades da presenza de varias enfermidades. $P(a,b,\lambda )=P(a|\lambda )P(b|\lambda )P(\lambda )\,$,         Eq.(6)

Advertencia de táboa

Como

{{{2}}}

 

 

 

 

({{{3}}})

se implementa como unha táboa, poñer

{{{2}}}

 

 

 

 

({{{3}}})

dentro dunha táboa rende unha táboa aniñada. Debido a un bug no manexo das táboas aniñadas de MediaWiki, {{NumBlk}} debe usarse con coidado neste caso. En concreto, cando se desexa unha indentación para a táboa externa, use a etiqueta explícita <dl><dd>...</dd></dl> para a indentación en vez de dous puntos (:) iniciais.

Por exemplo,

Markup	<dl><dd> {| |<math>(f * g)[n]\,</math>&nbsp; &nbsp; &nbsp; |{{NumBlk||<math>\stackrel{\mathrm{def}}{=}\sum_{m=-\infty}^{\infty} f[m]\cdot g[n - m]\,</math>| 3=<span style="color:darkred">'''(Ec.1)'''</span>|RawN=.}} |- | |<math>= \sum_{m=-\infty}^{\infty} f[n-m]\cdot g[m].\,</math> &nbsp; &nbsp; &nbsp; (commutatividade) |} </dd></dl>
Dá lugar a	$(f*g)[n]\,$      ${\stackrel {\mathrm {def} }{=}}\sum _{m=-\infty }^{\infty }f[m]\cdot g[n-m]\,$         (Ec.1) $=\sum _{m=-\infty }^{\infty }f[n-m]\cdot g[m].\,$       (commutatividade)

que mostra como as etiquetas externas <dl><dd>...</dd></dl> dan a mesma indentación que un só signo de dous puntos (:) que precede á táboa.

Para este outro exemplo,

Markup	<dl><dd> <dl><dd> {| |- |O primeiro parámetro para a indentación aínda funciona cando se usa dentro da táboa. {{NumBlk|::::|<math>ax^2+bx+c=0</math>|Nivel 4}} {{NumBlk|:::|<math>ax^2+bx+c=0</math>|Nivel 3}} {{NumBlk|::|<math>ax^2+bx+c=0</math>|Nivel 2}} {{NumBlk|:|<math>ax^2+bx+c=0</math>|Nivel 1}} {{NumBlk||<math>ax^2+bx+c=0</math>|Nivel 0}} |- |} </dd></dl> </dd></dl>
Aparece así	O primeiro parámetro para a indentación aínda funciona cando se usa dentro da táboa. $ax^{2}+bx+c=0$         (Nivel 4) $ax^{2}+bx+c=0$         (Nivel 3) $ax^{2}+bx+c=0$         (Nivel 2) $ax^{2}+bx+c=0$         (Nivel 1) $ax^{2}+bx+c=0$         (Nivel 0)

o cal usa dous conxuntos de etiquetas explícitas para dar a mesma indentación con dous puntos repetidos (::). Modelo:Basepage subpage

[ máis información | ver o historial | | | ver as instrucións ]

Este recadro non aparecerá no artigo.

Esta documentación está transcluída desde Modelo:Bloque numerado/uso. Os editores poden probar cambios no mesmo en Modelo:Bloque numerado/probas.
Por favor, engade as categorías na subpáxina de documentación e os interwikis no Wikidata. Ver as subpáxinas deste modelo.