Na Galipedia, a Wikipedia en galego.
A secante , é a razón trigonométrica recíproca do coseno :
sec
α
=
1
cos
α
=
c
b
{\displaystyle \sec \alpha ={\frac {1}{\cos \alpha }}={\frac {c}{b}}}
Temos que, calculando a partir da circunferencia de raio unidade:
sec
α
=
A
B
¯
A
C
¯
=
A
E
¯
A
D
¯
=
A
E
¯
1
=
A
E
¯
{\displaystyle \sec \alpha ={\frac {\overline {AB}}{\overline {AC}}}={\frac {\overline {AE}}{\overline {AD}}}={\frac {\overline {AE}}{1}}={\overline {AE}}}
Partindo da definición de secante como a recíproca do coseno:
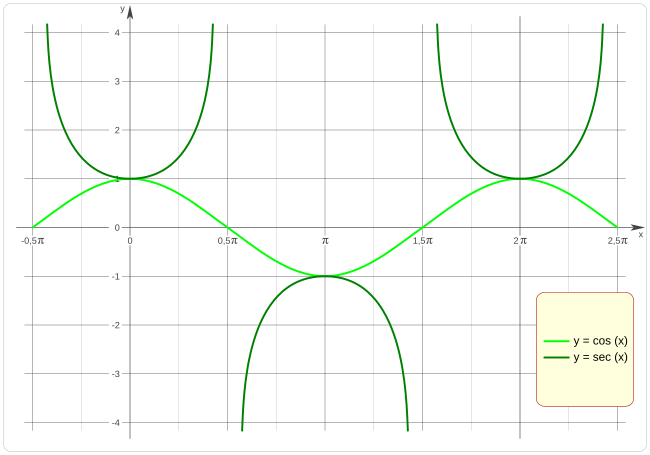
Coñecendo a función do coseno, podemos ver que para os valores nos que o coseno vale cero, a secante faise infinito, se a función coseno tende a cero desde valores positivos a secante tende a:
+
∞
{\displaystyle +\infty }
lim
α
→
π
2
−
cos
(
α
)
=
0
+
{\displaystyle \lim _{\alpha \to {\frac {\pi }{2}}^{-}}\cos(\alpha )=0^{+}}
lim
α
→
π
2
−
sec
(
α
)
=
1
lim
α
→
π
2
−
cos
(
α
)
=
1
0
+
=
+
∞
{\displaystyle \lim _{\alpha \to {\frac {\pi }{2}}^{-}}\sec(\alpha )={\cfrac {1}{{\underset {\alpha \to {\frac {\pi }{2}}^{-}}{\lim }}\;\cos(\alpha )}}={\cfrac {1}{0^{+}}}=+\infty }
mentres que cando o coseno tende a cero desde valores negativos a secante tende a:
−
∞
{\displaystyle -\infty }
lim
α
→
π
2
+
cos
(
α
)
=
0
−
{\displaystyle \lim _{\alpha \to {\frac {\pi }{2}}^{+}}\cos(\alpha )=0^{-}}
lim
α
→
π
2
+
sec
(
α
)
=
1
lim
α
→
π
2
+
cos
(
α
)
=
1
0
−
=
−
∞
{\displaystyle \lim _{\alpha \to {\frac {\pi }{2}}^{+}}\sec(\alpha )={\cfrac {1}{{\underset {\alpha \to {\frac {\pi }{2}}^{+}}{\lim }}\;\cos(\alpha )}}={\cfrac {1}{0^{-}}}=-\infty }
Cando o coseno do ángulo vale un, a súa secante tamén vale un, como se pode ver na gráfica.
Pódese obter facilmente unha táboa con algúns valores significativos lembrando que
sec
x
=
1
cos
x
{\displaystyle \sec x={1 \over \cos x}}
[ 1]
x
{\displaystyle x}
radiáns
0
π
12
{\displaystyle {\frac {\pi }{12}}}
π
6
{\displaystyle {\frac {\pi }{6}}}
π
4
{\displaystyle {\frac {\pi }{4}}}
π
3
{\displaystyle {\frac {\pi }{3}}}
5
12
π
{\displaystyle {\frac {5}{12}}\pi }
π
2
{\displaystyle {\frac {\pi }{2}}}
π
{\displaystyle \pi }
3
π
2
{\displaystyle {\frac {3\pi }{2}}}
2
π
{\displaystyle 2\pi }
x
{\displaystyle x}
graos 0°
15°
30°
45°
60°
75°
90°
180°
270°
360°
sec
(
x
)
{\displaystyle \sec(x)}
1
{\displaystyle 1}
6
−
2
{\displaystyle {\sqrt {6}}-{\sqrt {2}}}
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
2
{\displaystyle {\sqrt {2}}}
2
{\displaystyle 2}
6
+
2
{\displaystyle {\sqrt {6}}+{\sqrt {2}}}
∄
{\displaystyle \nexists }
−
1
{\displaystyle -1}
∄
{\displaystyle \nexists }
1
{\displaystyle 1}
As derivadas obtéñense lembrando a súa definición e aplicando a regra do cociente[ 2]
d
d
x
sec
x
=
d
d
x
1
cos
x
=
sin
x
cos
2
x
=
sec
x
⋅
tan
x
.
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\sec x={\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {1}{\cos x}}={\frac {\sin x}{\cos ^{2}x}}=\sec x\cdot \tan x.}
d
2
d
x
2
sec
x
=
d
d
x
tan
x
cos
x
=
d
d
x
sin
x
cos
2
x
=
1
+
sin
2
x
cos
3
x
=
sec
3
x
(
1
+
sin
2
x
)
.
{\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\sec x={\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\tan x}{\cos x}}={\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\sin x}{\cos ^{2}x}}={\frac {1+\sin ^{2}x}{\cos ^{3}x}}=\sec ^{3}x\left(1+\sin ^{2}x\right).}
Consecuencia da primeira relación fundamental da trigonometría
(
cos
2
x
+
sin
2
x
=
1
)
{\displaystyle (\cos ^{2}x+\sin ^{2}x=1)}
cosecante :
c
o
s
e
c
2
x
+
sec
2
x
=
c
o
s
e
c
2
x
⋅
sec
2
x
{\displaystyle \mathrm {cosec} ^{2}x+\sec ^{2}x=\mathrm {cosec} ^{2}x\cdot \sec ^{2}x}
para todo
x
≠
k
π
2
{\displaystyle x\neq k{\pi \over 2}}
k
∈
Z
{\displaystyle k\in \mathbb {Z} }
A relación obtense facilmente dividindo a relación fundamental por
sin
2
x
⋅
cos
2
x
{\displaystyle \sin ^{2}x\cdot \cos ^{2}x}
↑ Paolo Baroncini, Roberto Manfredi, Ilaria Fragni (2012). Ghisetti e Corvi, ed. Lineamenti.Math Blu Volume 4 . ISBN 978-88-538-0432-7 . ↑ Massimo Bergamini, Anna Trifone, Graziella Barozzi. Zanichelli, 2009, ed. Base azul curso de Matemáticas-Tomo 5 . ISBN 978-88-08-03933-0 .
Cobo Mérida, Purificación (2008). Trigonometría, 4 ESO . Materiales Didacticos Bemal. ISBN 978-84-612-6049-2 .