Traballo (física)
En mecánica (en xeral, na Física), o traballo efectuado por unha forza aplicada sobre unha partícula nun certo desprazamento defínese como o produto escalar do vector forza polo vector desprazamento. O traballo é unha magnitude física escalar, e represéntase coa letra W (do inglés Work) para distinguilo da magnitude temperatura, normalmente representada coa letra T e do tempo, representado por t.
O traballo é, en xeral, dependente da traxectoria e, polo tanto, non constitúe unha variable de estado.
Expresión matemática
[editar | editar a fonte]O traballo dunha forza F pode calcularse de forma xeral a través da seguinte integral de liña:
- onde:
- F é o vector forza
- ds é o vector desprazamento infinitesimal
O traballo é unha magnitude escalar que pode ser positiva ou negativa. Cando a forza actúa na dirección do movemento, o traballo é positivo, isto é, engádeselle enerxía ao corpo ou sistema. Pola contra, unha forza na dirección oposta ao movemento retira enerxía do corpo ou sistema. O tipo de enerxía, ben enerxía cinética ou enerxía potencial, depende do sistema en consideración.
Como mostra a ecuación de riba, a existencia dunha forza non é sinónimo de realización de traballo. Para que tal aconteza, é necesario que haxa movemento do punto de aplicación da forza e que haxa unha compoñente non nula da forza na dirección do movemento. É por esta razón que aparece un produto escalar entre F e s. Por exemplo, un corpo en movemento circular uniforme (velocidade angular constante) está suxeito a unha forza centrípeta. Porén, esta forza non realiza traballo, visto que é perpendicular á traxectoria.
Esta definición é válida para calquera tipo de forza independentemente da súa orixe. Así, pode tratarse dunha forza de rozamento, gravidade, eléctrica, magnética etc.
Historia
[editar | editar a fonte]A antiga concepción grega da física limitabase a estática das máquinas simples (o equilibrio da forzas) e non incluía a dinámica nin o concepto de traballo. Durante o Renacemento, empezouse a estudar a dinámica das potencias mecánicas, como se denominaban as máquinas simples, dende o punto de vista da distancia que poderían levantar unha carga, ademais da forza que poderían aplicar, o que conduciu finalmente ao novo concepto de traballo mecánico. A teoría dinámica completa das máquinas simples foi elaborada polo científico italiano Galileo Galilei en 1600 en Le Meccaniche (Sobre a mecánica), na que mostrou a semellanza matemática subxacente das máquinas como amplificadores de forza[1][2] Foi o primeiro en explicar que as máquinas simples non crean enerxía, só a transforman.[1]
Unidades
[editar | editar a fonte]A unidade SI de traballo é o joule (J), que se define como o traballo realizado por unha forza dun newton (N) actuando ao longo dun metro (m) na dirección do movemento. O traballo pódese expresar igualmente en N.m, como se desprende desta definición. Estas son as unidades máis correntes, no entanto, na medida en que o traballo é unha forma de enerxía, por veces empréganse outras unidades, por exemplo:
- quilovatio-hora (kW·h)
- Cabalo de vapor·hora (CV·h)
Outras fórmulas
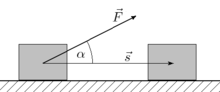
[editar | editar a fonte]Para o caso simple en que o corpo se traslada en movemento rectilíneo e a forza é paralela á dirección do movemento, o traballo vén dado pola fórmula:
onde F é a forza e s é a distancia percorrida polo corpo. Caso de que a forza se opoña ao movemento, o traballo é negativo. De forma máis xeral, a forza e o movemento poden tomarse como magnitudes vectoriais e combinarse a través do produto escalar:
Esta fórmula é válida para situacións en que a forza forma un ángulo coa dirección do movemento, mais presupón que a magnitude da forza e dirección do movemento sexan constantes. A xeneralización desta fórmula para situacións en que a forza e a dirección varían ao longo da traxectoria (ou do tempo) pode facerse recorrendo ao uso de diferenciais. O traballo infinitesimal dW realizado pola forza F ao longo do movemento infinitesimal ds ven entón dado por:
A integración de ambos os lados desta ecuación ao longo da traxectoria resulta na ecuación xeral inicialmente presentada.
Notas
[editar | editar a fonte]- ↑ 1,0 1,1 Krebs, Robert E. (2004). Groundbreaking Experiments, Inventions, and Discoveries of the Middle Ages. Greenwood Publishing Group. p. 163. ISBN 978-0-313-32433-8. Consultado o 21 de maio de 2008.
- ↑ Stephen, Donald; Lowell Cardwell (2001). Wheels, clocks, and rockets: a history of technology. US: W.W. Norton & Company. pp. 85–87. ISBN 978-0-393-32175-3.




