Coeficiente de Gini

O coeficiente de Gini é unha medida da desigualdade ideada polo estatístico italiano Corrado Gini publicada no documento "Variabilità e mutabilità" ("Variabilidade e mutabilidade" en italiano), en 1912. Normalmente utilízase para medir a desigualdade nos ingresos, dentro dun país, pero pode utilizarse para medir calquera forma de distribución desigual. O coeficiente de Gini é un número entre 0 e 1, onde 0 equivale á perfecta igualdade (todos teñen os mesmos ingresos) e o valor 1 correspóndese coa perfecta desigualdade (unha persoa ten todos os ingresos e os demais ningún). O índice de Gini é o coeficiente de Gini multiplicado por 100, é dicir, en porcentaxe, onde o 100 é o máximo, no canto de 1. Unha variación de dúas centésimas do coeficiente de Gini (ou dúas unidades do índice) equivale a unha distribución dun 7% de riqueza do sector máis pobre da poboación (por debaixo da mediana) ao máis rico (por derriba da mediana).

Aínda que o coeficiente de Gini utilízase sobre todo para medir a desigualdade nos ingresos, tamén pode utilizarse para medir a desigualdade na riqueza ou renda. Este uso require que ninguén dispoña dunha riqueza neta negativa.

Definición

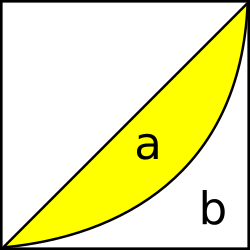
O coeficiente de Gini calcúlase como unha proporción das áreas no diagrama da curva de Lorenz. Se a área entre a liña de perfecta igualdade e a curva de Lorenz é a, e a área por debaixo da curva de Lorenz é b, entón o coeficiente de Gini é a/(a+b).

Esta proporción exprésase como porcentaxe ou como equivalente numérico desa porcentaxe, que é sempre un número entre 0 e 1. O coeficiente de Gini calcúlase a miúdo coa Fórmula de Brown, que é máis práctica:

$G=\left|1-\sum _{k=1}^{n-1}(X_{k+1}-X_{k})(Y_{k+1}+Y_{k})\right|$
Símbolo	Nome
$G$	Coeficiente de Gini
$X$	Proporción acumulada da variable poboación
$Y$	Proporción acumulada dos variable ingresos

De forma resumida, a Curva de Lorenz é unha gráfica de concentración acumulada da distribución da riqueza superposta á curva da distribución de frecuencias dos individuos que a posúen, e a súa expresión en porcentaxes é o índice de Gini.

Propiedades

Todas as curvas de Lorenz pasan pola recta ou a curva que une os puntos (0,0) e (1,1). A maior índice de Gini tense logo unha maior desigualdade. Se dúas curvas de Lorenz se cruzan entre si, recoméndase non sacar conclusións de carácter visual, xa que poden ser enganosas; é mellor comparar a desigualdade que representan, calculando primeiro os índices de Gini correspondentes a cada curva.
Para determinar a área entre a curva de Lorenz e a liña de perfecta equidade, o ideal é calcular unha integral definida, pero ás veces non se coñece a definición explícita da curva de Lorenz, polo que é interesante utilizar outras fórmulas cun número finito de sumandos.
As propiedades do índice de Gini son comparables coas do cadrado do coeficiente de variación.^[1]
Empiricamente, a renda de moitos países aproxímase a unha distribución Gamma (con parámetro k < 5), isto é, uns índices de Gini entre 0,50 e 0,25. Os países con índices superiores a 0,50 teñen unha distribución aínda máis desigual que a distribución exponencial.

Notas

↑ González Abril, Luis; Velasco-Morente, Francisco; Gavilán Ruiz, José Manuel; Sánchez-Reyes Fernández, Luis María (2010-12). "The similarity between the square of the coefficient of variation and the Gini index of a general random variable" (en inglés). ISSN 1886-516X. Arquivado dende o orixinal o 20 de abril de 2021. Consultado o 14 de marzo de 2022.

Véxase tamén

Bibliografía

Fedriani, E.M.; Martín, A.M. (2009). "Distribución personal y funcional de la renta". Economía Española (2.ª ed.). Madrid: McGraw-Hill/Interamericana de España SAU. pp. 331–345. ISBN 978-84-481-6806-3.
Fernández Montt, René (2011). Concentración de la Propiedad en Latinoamérica.
An Overview of Growing Income Inequalities in OECD Countries:Main Findings (PDF). OCDE. Dic-2011. Arquivado dende o orixinal (PDF) o 4 de xaneiro de 2012.

Outros artigos

Ligazóns externas

Calcular o Coeficiente Gini en R (en castelán)
UNITED NATIONS DEVELOPMENT PROGRAMME. Human Development Reports (en dez idiomas)
Vídeo explicativo. Midiendo la desigualdad: la curva de Lorenz y el índice de Gini
La distribución de la renta, la curva de Lorenz y el índice de Gini
Calculadora (en inglés): http://www.poorcity.richcity.org/calculator
Folla de cálculo (en inglés)
(en inglés) A complete handhout^{[Ligazón morta]} about the Lorenz curve including various applications, including an Excel spreadsheet graphing Lorenz curves and calculating Gini coefficients as well as coefficients of variation.
Folla de cálculo Excel que calcula o Índice de Gini, o Índice de Theil, a Redundancia, a Redundancia relativa, e representa a Curva de Lorenz: http://trucosexcel.blogspot.com/2011/05/indice-de-gini.html (en castelán)
Listagem do índice de Gini nos municípios do Brasil - IBGE

[1] González Abril, Luis; Velasco-Morente, Francisco; Gavilán Ruiz, José Manuel; Sánchez-Reyes Fernández, Luis María (2010-12). "The similarity between the square of the coefficient of variation and the Gini index of a general random variable" (en inglés). ISSN 1886-516X. Arquivado dende o orixinal o 20 de abril de 2021. Consultado o 14 de marzo de 2022.

[1]