Criba de Eratóstenes
En matemáticas, a criba de Eratóstenes é un algoritmo antigo para atopar todos os números primos ata un límite determinado.
Faino marcando iterativamente como compostos (é dicir, non primos) os múltiplos de cada número primo, comezando polo primeiro número primo, 2. Os múltiplos dun número primo dado xéranse como unha secuencia de números a partir dese primo, cunha diferenza constante entre eles que é igual a ese primo.[1] Esta é a distinción clave da criba coa división de proba na que se proba secuencialmente cada número candidato dividindo polos primos.[2] Unha vez marcados como compostos todos os múltiplos de cada primo, os restantes números sen marcar son primos.
Esta é unha das varias cribas de números primos, sendo unha das formas máis eficientes para atopar os números primos máis pequenos. Pódese usar tamén para atopar números primos en progresións aritméticas.[3]
Exemplo
[editar | editar a fonte]Para atopar todos os números primos inferiores ou iguais a 30, proceda do seguinte xeito.
En primeiro lugar, xera unha lista de números enteiros do 2 ao 30:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
O primeiro número da lista é 2; risca todos os pares, pois son múltiplos de 2.
2 3456789101112131415161718192021222324252627282930
O seguinte número da lista despois de 2 é 3; risca cada 3 números da lista despois de 3 contando a partir de 3 en incrementos de 3 (son os múltiplos de 3 da lista):
2 3456789101112131415161718192021222324252627282930
O seguinte número aínda non riscado na lista despois do 3 é o 5; riscamos o 5 e o seguinte contando 5 (é dicir, todos os múltiplos de 5):
2 3456789101112131415161718192021222324252627282930
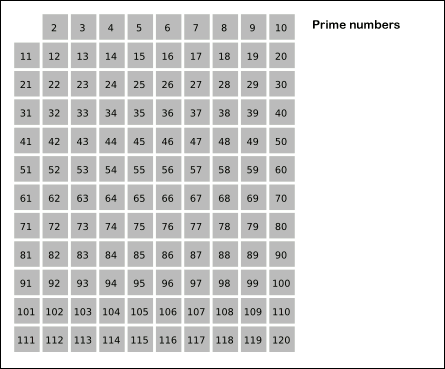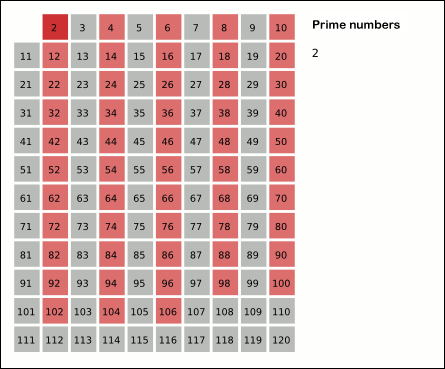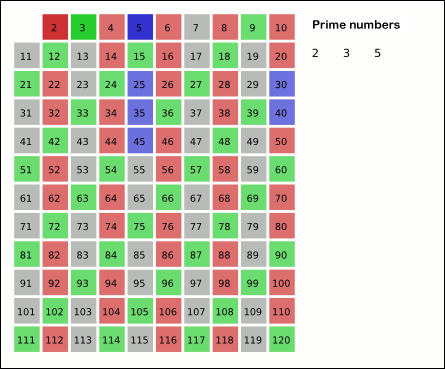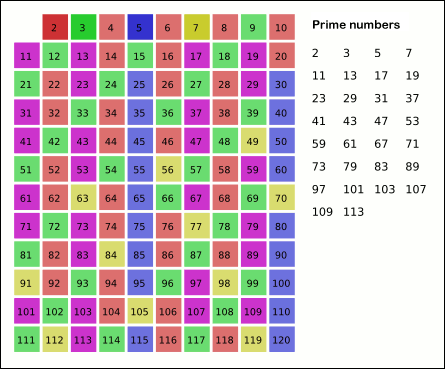
O seguinte número aínda non riscado na lista despois do 5 é o 7; facemos igual que antes cos múltiplos de 7, mais xa están todos riscados neste momento, xa que estes números (14, 21, 28) tamén son múltiplos de números primos máis pequenos porque 7 × 7 é maior que 30. Os números non riscados neste punto da lista son todos os números primos inferiores a 30:
2 3 5 7 11 13 17 19 23 29
Algoritmo e variantes
[editar | editar a fonte]Este algoritmo produce todos os números primos non superiores a n. Pódese incluír unha optimización común, que consiste en comezar a enumerar os múltiplos de cada primo i a partir de i2. A complexidade temporal deste algoritmo é O(n log log n),[4] sempre que a actualización da matriz sexa unha operación O(1), como adoita ser o caso.
Criba segmentada
[editar | editar a fonte]Como sinala Sorenson, o problema da criba de Eratóstenes non é o número de operacións que realiza senón os seus requisitos de memoria.[4] Para un n grande, o intervalo de números primos pode non caber na memoria; peor aínda, mesmo para n moderado, o seu uso da caché é moi subóptimo. O algoritmo percorre toda a matriz A, sen case ningunha localización de referencia.
Unha solución a estes problemas oferécense mediante cribas segmentadas, onde só se criban porcións do intervalo de cada vez.[5] Estes algoritmos coñécense dende os anos 70.
Criba incremental
[editar | editar a fonte]Unha formulación incremental da criba [2] xera números primos indefinidamente (é dicir, sen límite superior) ao intercalar a xeración de primos coa xeración dos seus múltiplos (de xeito que os primos poden atoparse nos espazos entre os múltiplos), onde os múltiplos de cada p primo xéranse directamente contando a partir do cadrado do primo en incrementos de p (ou 2p para números primos impares). A xeración debe iniciarse só cando se alcance o cadrado do primo, para evitar efectos adversos sobre a eficiencia.
Ao probar un primo individualmente, o algoritmo óptimo de proba de división usa todos os números primos que non excedan a súa raíz cadrada, mentres que a criba de Eratóstenes produce cada composto só a partir dos seus factores primos e obtén os primos "de balde" entre os compostos.
Complexidade algorítmica
[editar | editar a fonte]A criba de Eratóstenes é unha forma popular de comparar o rendemento dos ordenadores.[6] A complexidade temporal de calcular todos os números primos por debaixo de n nunha máquina de acceso aleatorio é O(n log log n) operacións, unha consecuencia directa do feito de que a serie harmónica de primos se aproxima asintóticamente a log log n . No entanto, ten unha complexidade temporal exponencial en relación á lonxitude da entrada, o que o converte nun algoritmo pseudopolinomial. O algoritmo básico require O(n) de memoria.
Criba de Euler
[editar | editar a fonte]A proba da fórmula do produto de Euler da función zeta contén unha versión da criba de Eratóstenes na que cada número composto se elimina exactamente unha vez.[4] A mesma criba foi redescuberta e observouse que levaba tempo linear por Gries & Misra (1978). Tamén comeza cunha lista de números do 2 ao n ordenados. En cada paso o primeiro elemento identifícase como o seguinte primo, multiplícase con cada elemento da lista (comenzando así por si mesmo), e os resultados márcanse na lista para a súa posterior eliminación. O elemento inicial e os elementos marcados sácanse logo da secuencia de traballo e repítese o proceso:
[2] (3) 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 7 6 7 7 6 7 7 6 7 [3] (5) 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 ... [4] (7) 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79 ... [5] (11) 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 ... [...]
Notas
[editar | editar a fonte]- ↑ Horsley, Rev. Samuel, F. R. S., "Κόσκινον Ερατοσθένους or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers," Philosophical Transactions (1683–1775), Vol. 62. (1772), pp. 327–347.
- ↑ 2,0 2,1 O'Neill, Melissa E., "The Genuine Sieve of Eratosthenes", Journal of Functional Programming, published online by Cambridge University Press 9 October 2008 doi 10.1017/S0956796808007004, pp. 10, 11 (contains two incremental sieves in Haskell: a priority-queue–based one by O'Neill and a list–based, by Richard Bird).
- ↑ J. C. Morehead, "Extension of the Sieve of Eratosthenes to arithmetical progressions and applications", Annals of Mathematics, Second Series 10:2 (1909), pp. 88–104.
- ↑ 4,0 4,1 4,2 Jonathan Sorenson, An Introduction to Prime Number Sieves, Computer Sciences Technical Report #909, Department of Computer Sciences University of Wisconsin-Madison, January 2, 1990 (the use of optimization of starting from squares, and thus using only the numbers whose square is below the upper limit, is shown).
- ↑ Crandall & Pomerance, Prime Numbers: A Computational Perspective, second edition, Springer: 2005, pp. 121–24.
- ↑ Peng, T. A. (Fall 1985). "One Million Primes Through the Sieve". BYTE: 243–244. Consultado o 19 March 2016.
Véxase tamén
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Criba de Eratóstenes |
Outros artigos
[editar | editar a fonte]Ligazóns externas
[editar | editar a fonte]- primesieve – Very fast highly optimized C/C++ segmented Sieve of Eratosthenes
- Eratosthenes, sieve of at Encyclopaedia of Mathematics
- Interactive JavaScript Page
- Sieve of Eratosthenes by George Beck, Wolfram Demonstrations Project.
