Función de activación

A función de activación dun nodo nunha rede neural artificial é unha función que calcula a saída do nodo baseándose nas súas entradas individuais e os seus pesos. Os problemas non triviais poden ser solucionados utilizando só uns cantos nodos se a función de activación é non linear.^[1] As funcións de activación modernas inclúen a versión suave da ReLU, a GELU, o cal foi utilizado no 2018 modelo BERT, a función loxística (sigmoide) utilizada no modelo de recoñecemento da fala de 2012 desenvolvido por Hinton et al., a ReLU utilizada no modelo de visión por computador AlexNet de 2012 e no modelo ResNet de 2015.^[2]^[3]^[4]

Comparación de funcións de activación

Á parte do seu rendemento empírico, as funcións de activacións tamén teñen propiedades matemáticas diferentes:

Non linear: Cando a función de activación é non linear, pódese probar que unha rede neural de dúas capas pode ser un aproximador universal de funcións.^[5] Isto coñécese como o teorema de aproximación universal. A función de activación identidade non satisfai esta propiedade. Cando múltiples capas utilizan a función de activación identidade, toda a rede é equivalente a un modelo dunha única capa.
Imaxe: Cando a imaxe da función de activación é finita, os métodos de adestramento baseados non descenso do gradiente tenden a ser máis estables, porque as presentacións de patróns afectan de forma significativa só a un número limitado de pesos. Cando a imaxe é infinita, o adestramento é xeralmente máis eficiente porque as presentacións de patróns afectan de forma significativa á maioría dos pesos. No caso último, tipicamente son necesarios taxas de aprendizaxe máis pequenas.
Continuamente diferenciable: Esta propiedade é desexable (ReLU non é continuamente diferenciable e ten algúns problemas coa optimización baseada en gradientes, mais aínda é posible) para os métodos de optimización baseados no gradiente. A función de activación do paso binario non é diferenciable no 0, e a súa derivada é 0 no resto de valores, polo que os métodos baseados no gradiente non poden facer ningún progreso con ela.^[6]

Estas propiedades non inflúen decisivamente no rendemento, nin son as únicas propiedades matemáticas que poden ser útiles. Por exemplo, a imaxe estritamente positiva da función de activación suave positiva faina adecuada para predicir varianzas en auto-codificadores variacionais.

Aspectos matemáticos

As funcións de activación máis comúns poden dividirse en tres categorías: funcións de crista, funcións radiais e funcións de prego.

Unha función de activación $f$ considérase saturante se $\lim _{|v|\to \infty }|\nabla f(v)|=0$ . É non saturante se $\lim _{|v|\to \infty }|\nabla f(v)|\neq 0$ . As funcións de activación non saturantes, como ReLU, poden ser mellores que as saturantes, porque son menos propensas a sufrir o problema do esvaecemento do gradiente.^[3]

Funcións de activación de crista

As funcións de crista son funcións de varias variables que actúan sobre unha combinación linear das variables de entrada. Algúns exemplos utilizados a miúdo son os seguintes:

Función de activación linear: $\phi (\mathbf {v} )=a+\mathbf {v} '\mathbf {b}$
Función de activación ReLU: $\phi (\mathbf {v} )=\max(0,a+\mathbf {v} '\mathbf {b} )$
Función de activación Heaviside: $\phi (\mathbf {v} )=1_{a+\mathbf {v} '\mathbf {b} >0}$
Función de activación loxística: $\phi (\mathbf {v} )=(1+\exp(-a-\mathbf {v} '\mathbf {b} ))^{-1}$

En redes neurais inspiradas na bioloxía, a función de activación é normalmente unha abstracción que representa a taxa de impulso de potenciais de acción na célula.^[7] Na súa forma máis sinxela, esta función é binaria, é dicir, ou a neurona está nun impulso ou non. As neuronas tampouco poden facer impulsos máis rápido que un determinado valor, motivando as funcións de activación sigmoides, cuxa imaxe é un intervalo finito.

A función é a seguinte, $\phi (\mathbf {v} )=U(a+\mathbf {v} '\mathbf {b} )$ $U$ , onde $U$ é a función de paso Heaviside.

Se unha liña ten unha pendente positiva, pode reflectir o aumento na taxa de impulsos que ocorre a medida que aumenta a corrente de entrada. Tal función sería da forma $\phi (\mathbf {v} )=a+\mathbf {v} '\mathbf {b}$ .

Funcións de activación radiais

Unha clase especial de funcións de activación son as funcións radiais básicas (RBFs, das súas siglas en inglés), utilizadas en redes de RBF, as cales son extremadamente eficientes como aproximadores universais de funcións. Estas funcións de activación poden tomar moitas formas, pero normalmente atópanse como algunha das funcións seguintes:

Función gaussiana: $\,\phi (\mathbf {v} )=\exp \left(-{\frac {\|\mathbf {v} -\mathbf {c} \|^{2}}{2\sigma ^{2}}}\right)$
Función multicadrática: $\,\phi (\mathbf {v} )={\sqrt {\|\mathbf {v} -\mathbf {c} \|^{2}+a^{2}}}$
Función multicadrática inversa: $\,\phi (\mathbf {v} )=\left(\|\mathbf {v} -\mathbf {c} \|^{2}+a^{2}\right)^{-{\frac {1}{2}}}$
Splines poliharmónicos

Onde $\mathbf {c}$ é o vector representando o centro da función e $a$ e $\sigma$ os parámetros que afectan á dispersión do radio.

Funcións de activación de prego

As funcións de activación de prego son amplamente usadas nas capas de agrupamento nas redes neurais convolucionais e en capas de saída de redes de clasificación multiclases. Estas funcións de activación realizan agregación sobre as entradas, como tomar a media, mínimo ou máximo. En problemas de clasificación multiclase, utilízase con frecuencia a función de activación softmax.

Táboa de funcións de activación

A seguinte táboa compara as propiedades de varias funcións de activación:

Nome	Función, $g(x)$	Derivada de $g$ , $g'(x)$	Rango	Diferenciabilidade
Identidade	$x$	$1$	$(-\infty ,\infty )$	$C^{\infty }$
Paso binario	${\begin{cases}0&{\text{se }}x<0\\1&{\text{se }}x\geq 0\end{cases}}$	$0$	$\{0,1\}$	$C^{-1}$
Loxística, sigmoide ou paso suave	$\sigma (x)\doteq {\frac {1}{1+e^{-x}}}$	$g(x)(1-g(x))$	$(0,1)$	$C^{\infty }$
Tanxente hiperbólica (tanh)	$\tanh(x)\doteq {\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$	$1-g(x)^{2}$	$(-1,1)$	$C^{\infty }$
Tanxente hiperbólica de Soboleva (smht)	$\operatorname {smht} (x)\doteq {\frac {e^{ax}-e^{-bx}}{e^{cx}+e^{-dx}}}$		$(-1,1)$	$C^{\infty }$
Unidade linear rectificada (ReLU)	${\begin{aligned}(x)^{+}\doteq {}&{\begin{cases}0&{\text{se }}x\leq 0\\x&{\text{se }}x>0\end{cases}}\\={}&\max(0,x)=x{\textbf {1}}_{x>0}\end{aligned}}$	${\begin{cases}0&{\text{se }}x<0\\1&{\text{se }}x>0\end{cases}}$	$[0,\infty )$	$C^{0}$
Unidade linear de erro gaussiano (GELU)	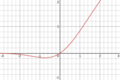${\begin{aligned}&{\frac {1}{2}}x\left(1+{\text{erf}}\left({\frac {x}{\sqrt {2}}}\right)\right)\\{}={}&x\Phi (x)\end{aligned}}$	$\Phi (x)+x\phi (x)$	$(-0.17\ldots ,\infty )$	$C^{\infty }$
Suave positiva^[8]	$\ln \left(1+e^{x}\right)$	${\frac {1}{1+e^{-x}}}$	$(0,\infty )$	$C^{\infty }$
Unidade linear exponencial (ELU)	${\begin{cases}\alpha \left(e^{x}-1\right)&{\text{se }}x\leq 0\\x&{\text{se }}x>0\end{cases}}$ Con parámetro $\alpha$	${\begin{cases}\alpha e^{x}&{\text{se }}x<0\\1&{\text{se }}x>0\end{cases}}$	$(-\alpha ,\infty )$	${\begin{cases}C^{1}&{\text{se }}\alpha =1\\C^{0}&{\text{noutro caso}}\end{cases}}$
Unidade linear exponencial escalada (SELU)^[9]	$\lambda {\begin{cases}\alpha (e^{x}-1)&{\text{se }}x<0\\x&{\text{se }}x\geq 0\end{cases}}$ Con parámetros $\lambda =1.0507$ e $\alpha =1.67326$	$\lambda {\begin{cases}\alpha e^{x}&{\text{se }}x<0\\1&{\text{se }}x\geq 0\end{cases}}$	$(-\lambda \alpha ,\infty )$	$C^{0}$
Unidade linear rectificada con fuga (Leaky ReLU)^[10]	${\begin{cases}0.01x&{\text{se }}x\leq 0\\x&{\text{se }}x>0\end{cases}}$	${\begin{cases}0.01&{\text{se }}x<0\\1&{\text{se }}x>0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$
Unidade linear rectificada paramétrica (PReLU)	${\begin{cases}\alpha x&{\text{se }}x<0\\x&{\text{se }}x\geq 0\end{cases}}$ Con parámetro $\alpha$	${\begin{cases}\alpha &{\text{se }}x<0\\1&{\text{se }}x\geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$
Unidade linear sigmoide (SiLU)^[11]	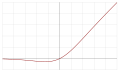${\frac {x}{1+e^{-x}}}$	${\frac {1+e^{-x}+xe^{-x}}{\left(1+e^{-x}\right)^{2}}}$	$[-0.278\ldots ,\infty )$	$C^{\infty }$
Gaussiana	$e^{-x^{2}}$	$-2xe^{-x^{2}}$	$(0,1]$	$C^{\infty }$

A seguinte táboa lista funcións de activación que non son funcións dun só prego $x$ da capa ou capas anteriores:

Nome	Función, $g_{i}\left({\vec {x}}\right)$	Derivada, ${\frac {\partial g_{i}\left({\vec {x}}\right)}{\partial x_{j}}}$	Imaxe	Diferenciabilidade
Softmax	${\frac {e^{x_{i}}}{\sum _{j=1}^{J}e^{x_{j}}}}$ , $i$ = 1, …, $J$	$g_{i}\left({\vec {x}}\right)\left(\delta _{ij}-g_{j}\left({\vec {x}}\right)\right)$ ^[1]	$(0,1)$	$C^{\infty }$
Maxout^[12]	$\max _{i}x_{i}$	${\begin{cases}1&{\text{se }}j={\underset {i}{\operatorname {argmax} }}\,x_{i}\\0&{\text{se }}j\neq {\underset {i}{\operatorname {argmax} }}\,x_{i}\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$

^ Aquí,

\delta _{ij}

é a Delta de Kronecker.

Funcións de activación cuánticas

Nas redes neurais cuánticas programadas en computadoras cuánticas de modelo de porta, baseadas en perceptróns cuánticos en lugar de circuítos cuánticos variacionales, a non linearidade da función de activación pódese implementar sen necesidade de medir a saída de cada perceptrón en cada capa. As propiedades cuánticas cargadas dentro do circuíto, como a superposición, poden ser preservadas creando a serie de Taylor do argumento calculado polo propio perceptrón, con circuítos cuánticos axeitados que calculan as potencias ata un grao de aproximación desexado. Debido á flexibilidade de ditos circuítos cuánticos, poden ser deseñados para aproximar calquera función de activación clásica arbitraria.^[13]

Vantaxes e inconvenientes dalgunhas funcións de activación

Sigmoide

Esta función de activación presenta numerosos inconvenientes, tales como que a saída non está centrada no cero (o que deriva en problemas coa actualización de pesos polas direccións do gradiente), que as neuronas saturadas "matan" ao gradiente e que a operación expoñencial é cara computacionalmente.

Tanxente hiperbólica

Neste caso, a tanxente hiperbólica si que está centrada no cero. Malia isto, comparte o resto de desvantaxes coa función sigmoide.

ReLU

Esta función de activación non satura (pois é positiva), é eficiente computacionalmente e ten unha converxencia rápida (ao redor de 6 veces máis rápida que as dúas funcións anteriores). Porén, a saída non está centrada no cero e as neuronas poden morrer (polo que hai que escoller unha taxa de aprendizaxe axeitada, xeralmente baixa).

ReLU con fuga

Nesta función as neuronas non morren e a media das saídas está cerca do cero, alén de ter tódalas vantaxes da ReLU.

Maxout

Nesta función de activación as neuronas tampouco morren, mais o número de parámetros dóbrase.

ELU

Esta función ten tódalas vantaxes da ReLU salvo o seu tempo de cómputo, pois utiliza a aplicación expoñencial, que demora os cálculos.^[14]

Notas

↑ Hinkelmann, Knut. "Neural Networks" (PDF). University of Applied Sciences Northwestern Switzerland. Arquivado dende o orixinal (PDF) o 06 de outubro de 2018. Consultado o 17 de agosto de 2024.
↑ Hinton, Geoffrey; Deng, Li; Yu, Dong; Dahl, George; Mohamed, Abdel-rahman; Jaitly, Navdeep; Senior, Andrew; Vanhoucke, Vincent; Nguyen, Patrick (2012). "Deep Neural Networks for Acoustic Modeling in Speech Recognition". IEEE Signal Processing Magazine 29: 82.97. doi:10.1109/MSP.2012.2205597.
↑ ^3,0 ^3,1 Krizhevsky, Alex; Sutskever, Ilya; Hinton, Geoffrey E. (24-05-2017). "ImageNet classification with deep convolutional neural networks". Communications of the ACM 60: 84–90. ISSN 0001-0782. doi:10.1145/3065386. |data-acceso= require |url= (Axuda)
↑ Al-johania, Norah; Elrefaei, Lamiaa (30-06-2019). "Dorsal Hand Vein Recognition by Convolutional Neural Networks: Feature Learning andn Transfer Learning Approaches" (PDF). International Journal of Intelligent Engineering and Systems 12: 178–191. doi:10.22266/ijies2019.0630.19.
↑ Cybenko, G. (Decembro 1989). "Approximation by superpositions of a sigmoidal function" (PDF). Mathematics of Control, Signals, and Systems (en inglés) 2: 303–314. ISSN 0932-4194. doi:10.1007/BF02551274.
↑ Snyman, Jan (03-03-2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Science & Business Media. ISBN 978-0-387-24348-1.
↑ Hodgkin, A. L.; Huxley, A. F. (28-08-1952). "A quantitative description of membrane current and its applicatiton to conduction and excitation in nerve". The Journal of Physiology 117: 500–544. PMC 1392413. PMID 12991237. doi:10.1113/jphysiol.1952.sp004764.
↑ Glorot, Xavier; Bordes, Antoine; Bengio, Yoshua (2011). "Deep sparse rectifier neural networks" (PDF). International Conference on Artificial Intelligence and Statistics.
↑ Klambauer, Günter; Unterthiner, Thomas; Mayr, Andreas; Hochreiter, Sepp (08-06-2017). "Self-Normalizing Neural Networks". Advances in Neural Information Processing Systems 30. arXiv:1706.02515.
↑ Maas, Andrew; Jannun, Awni Y.; Ng, Andrew Y. (Xuño 2013). "Rectifier nonlinearities improve neural nertwork acoustic models". Proc. ICML 30.
↑ Elfwing, Stefan; Uchibe, Eiji; Doya, Kenji (2018). "Sigmoid-Weighted Linera Units for Neural Network Function Approximation in Reinforcement Learning". Neural Networks 107: 3–11. PMID 29395652. arXiv:1702.03118. doi:10.1016/j.neunet.2017.12.012.
↑ Goodfellow, Ian J.; Warde-Farley, David; Mirza, Mehdi; Courville, Aaron; Bengio, Yochua (2013). "Maxout Networks". JMLR Workshop and Conference Proceedings 28: 1319–1327. arXiv:1302.4389.
↑ Maronese, Marco; Destri, Claudio; Prati, Enrico (2022). "Quantum activation functions for quantum neural networks". Quantum Information Processing 21. Bibcode:2022QuIP...21..128M. ISSN 1570-0755. arXiv:2201.03700. doi:10.1007/s11128-022-03466-0.
↑ Li, Fei Fei; Johnson, Justin; Yeung, Serena (2018). Convolutional Neural Networks for Visual Recognition. Stanford University.

Véxase tamén

Outros artigos

[1] Hinkelmann, Knut. "Neural Networks" (PDF). University of Applied Sciences Northwestern Switzerland. Arquivado dende o orixinal (PDF) o 06 de outubro de 2018. Consultado o 17 de agosto de 2024.

[2] Hinton, Geoffrey; Deng, Li; Yu, Dong; Dahl, George; Mohamed, Abdel-rahman; Jaitly, Navdeep; Senior, Andrew; Vanhoucke, Vincent; Nguyen, Patrick (2012). "Deep Neural Networks for Acoustic Modeling in Speech Recognition". IEEE Signal Processing Magazine 29: 82.97. doi:10.1109/MSP.2012.2205597.

[:0-3] 3,0 ^3,1 Krizhevsky, Alex; Sutskever, Ilya; Hinton, Geoffrey E. (24-05-2017). "ImageNet classification with deep convolutional neural networks". Communications of the ACM 60: 84–90. ISSN 0001-0782. doi:10.1145/3065386. |data-acceso= require |url= (Axuda)

[4] Al-johania, Norah; Elrefaei, Lamiaa (30-06-2019). "Dorsal Hand Vein Recognition by Convolutional Neural Networks: Feature Learning andn Transfer Learning Approaches" (PDF). International Journal of Intelligent Engineering and Systems 12: 178–191. doi:10.22266/ijies2019.0630.19.

[5] Cybenko, G. (Decembro 1989). "Approximation by superpositions of a sigmoidal function" (PDF). Mathematics of Control, Signals, and Systems (en inglés) 2: 303–314. ISSN 0932-4194. doi:10.1007/BF02551274.

[6] Snyman, Jan (03-03-2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Science & Business Media. ISBN 978-0-387-24348-1.

[7] Hodgkin, A. L.; Huxley, A. F. (28-08-1952). "A quantitative description of membrane current and its applicatiton to conduction and excitation in nerve". The Journal of Physiology 117: 500–544. PMC 1392413. PMID 12991237. doi:10.1113/jphysiol.1952.sp004764.

[8] Glorot, Xavier; Bordes, Antoine; Bengio, Yoshua (2011). "Deep sparse rectifier neural networks" (PDF). International Conference on Artificial Intelligence and Statistics.

[9] Klambauer, Günter; Unterthiner, Thomas; Mayr, Andreas; Hochreiter, Sepp (08-06-2017). "Self-Normalizing Neural Networks". Advances in Neural Information Processing Systems 30. arXiv:1706.02515.

[10] Maas, Andrew; Jannun, Awni Y.; Ng, Andrew Y. (Xuño 2013). "Rectifier nonlinearities improve neural nertwork acoustic models". Proc. ICML 30.

[11] Elfwing, Stefan; Uchibe, Eiji; Doya, Kenji (2018). "Sigmoid-Weighted Linera Units for Neural Network Function Approximation in Reinforcement Learning". Neural Networks 107: 3–11. PMID 29395652. arXiv:1702.03118. doi:10.1016/j.neunet.2017.12.012.

[12] Goodfellow, Ian J.; Warde-Farley, David; Mirza, Mehdi; Courville, Aaron; Bengio, Yochua (2013). "Maxout Networks". JMLR Workshop and Conference Proceedings 28: 1319–1327. arXiv:1302.4389.

[13] Maronese, Marco; Destri, Claudio; Prati, Enrico (2022). "Quantum activation functions for quantum neural networks". Quantum Information Processing 21. Bibcode:2022QuIP...21..128M. ISSN 1570-0755. arXiv:2201.03700. doi:10.1007/s11128-022-03466-0.

[14] Li, Fei Fei; Johnson, Justin; Yeung, Serena (2018). Convolutional Neural Networks for Visual Recognition. Stanford University.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[1]

[12]

[13]

[14]