Teorema do seno

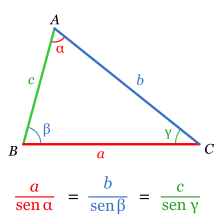
En trigonometría, o teorema do seno é unha relación de proporcionalidade entre as lonxitudes dos lados dun triángulo e os senos dos ángulos respectivamente opostos.

Se nun triángulo ABC, as medidas dos lados opostos aos ángulos A, B e C son respectivamente a, b, c, entón;

${\frac {a}{\operatorname {sen} \,A}}={\frac {b}{\operatorname {sen} \,B}}={\frac {c}{\operatorname {sen} \,C}}$

Demostración

A pesar de ser dos teoremas trigonométricos máis usados e de ter unha demostración particularmente simple, é pouco común que se presente.

Dado o triángulo ABC, denotamos por O o seu circuncentro e debuxamos a súa circunferencia circunscrita. Prolongando o segmento BO até cortar a circunferencia, obtense un diámetro BP.

Agora, o triángulo PBC é recto, posto que BP é un diámetro, e ademais os ángulos A e P son iguais, porque ambos son ángulos inscritos que abren o segmento BC (Véxase definición de arco capaz). Por definición da función trigonométrica seno, tense

$\operatorname {sen} \,A=\operatorname {sen} \,P={\frac {BC}{BP}}={\frac {a}{2R}}$

onde R é o radio da circunferencia. Despexando 2R obtemos:

${\frac {a}{\operatorname {sen} \,A}}=2R$

Repetindo o procedemento cun diámetro que pase por A e outro que pase por C, chégase a que as tres fraccións teñen o mesmo valor 2R e polo tanto son iguais.

A conclusión que se obtén acostuma chamarse teorema dos senos xeneralizado e establece que para un triángulo ABC onde a, b, c son os lados opostos aos ángulos A, B, C respectivamente, se R denota o radio da circunferencia circunscrita, entón:

${\frac {a}{\operatorname {sen} \,A}}={\frac {b}{\operatorname {sen} \,B}}={\frac {c}{\operatorname {sen} \,C}}=2R$

Pode enunciarse o teorema dunha forma alternativa:

Nun triángulo, o cociente entre cada lado e o seno do seu ángulo oposto é constante e igual ao diámetro da circunferencia circunscrita.

Aplicación

O teorema do seno é utilizado para resolver problemas nos que se coñecen dous ángulos do triángulo e un lado oposto a un deles. Tamén se usa cando coñecemos dous lados do triángulo e un ángulo oposto a un deles.

Relación coa área do triángulo

Para un triángulo ABC, a área calcúlase como ah/2 onde h é a medida da altura sobre a base a. Novamente, por definición de seno, tense sen C = h/b ou o que é o mesmo h = b sen C, de modo que se cumpre:

Area={\frac {a\;h}{2}}={\frac {a\;b\,\;\operatorname {sen} \,C}{2}}

.

Mais, o teorema dos senos implica que c = 2R sen C, polo que ao substituír na expresión anterior obtense un novo teorema: $Area={\frac {a\;h}{2}}={\frac {a\;b\,\;\operatorname {sen} \,C}{2}}={\frac {a\;b\;c}{4\;R}}$

Véxase tamén

Outros artigos