Teorema do valor intermedio

Non confundir con Teorema do valor medio.

Teorema do Valor Intermediario. Existe un $c$ pertencente a $(a,b)$ tal que $f(c)=d$

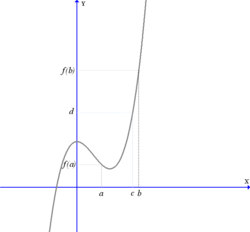
En análise real, o teorema do valor intermedio é unha propiedade das funcións continuas reais nun intervalo. O teorema establece que se unha función é continua nun intervalo, a función toma todos os valores intermedios comprendidos entre os valores da función nos extremos do intervalo.

Como consecuencia do teorema de Weierstrass pódese xeneralizar dicindo que a imaxe dun intervalo é outro intervalo, sendo os subconxuntos conexos dos números reais.

Enunciado

Sexa $f$ unha función continua nun intervalo $[a,b]$ e supoñamos que $f(a)<f(b)$. Entón para cada $d$ tal que $f(a)<d<f(b)$, existe un $c$ pertencente a $(a,b)$ tal que $f(c)=d$ . Obtense a mesma conclusión no caso que $f(b)<f(a)$.

Demostración

O teorema pode demostrarse facilmente aplicando o teorema de Bolzano (que se trata dun caso particular do teorema do valor intermedio).

Notas

• Bombal, Marin & Vera: Problemas de Análisis matemático: Cálculo Diferencial, 1988, ed. AC, ISBN 84-7288-101-6.
• Agudo, F. R. Dias, Análise Real (3 volumes), Lisboa: Escolar Editora, 1994
• Ostrowski, A., Lições de Cálculo Diferencial e Integral (3 volumes), Lisboa: Fundação Calouste Gulbenkian, 1981