Circunferencia goniométrica
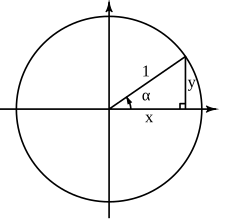
A circunferencia goniométrica[1], trigonométrica, unitaria, é unha circunferencia de raio [2], normalmente co seu centro na orixe dun sistema de coordenadas, dun plano euclidiano ou complexo. Devandita circunferencia utilízase co fin de poder estudar facilmente as razóns trigonométricas e funcións trigonométricas, mediante a representación de triángulos rectángulos auxiliares.
Se é un punto da circunferencia unidade do primeiro cuadrante, entón x e y son as lonxitudes dos catetos dun triángulo rectángulo cuxa hipotenusa ten lonxitude . Aplicando o Teorema de Pitágoras, e satisfán a seguinte ecuación: .
Funcións trigonométricas na circunferencia unitaria
[editar | editar a fonte]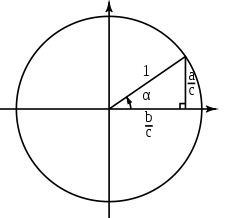

Se é un punto da circunferencia unidade, e o raio que ten a orixe en forma un ángulo co eixo , as principais funcións trigonométricas pódense representar como razón de segmentos asociados a triángulos rectángulos auxiliares, da seguinte maneira:
O seno é a razón entre o cateto oposto () e a hipotenusa ()
e dado que a hipotenusa é igual ao raio, que ten valor , dedúcese:
O coseno é a razón entre o cateto adxacente () e a hipotenusa ()
e como a hipotenusa ten valor , dedúcese:
A tanxente é a razón entre o cateto oposto e o adxacente


Por semellanza de triángulos: e como dedúcese que e, por tanto, .
Funcións trigonométricas recíprocas
[editar | editar a fonte]A cosecante, a secante e a cotanxente, son as razóns trigonométricas recíprocas do seno, coseno e tanxente:
Os valores da cotanxente, a secante e a cosecante obtéñense, analogamente, mediante semellanza de triángulos.
Topoloxía
[editar | editar a fonte]En topoloxía, a circunferencia unitaria (tamén denominada disco unidade) clasifícase como ; a xeneralización para unha dimensión máis é a esfera unidade [3].
Grupo circular
[editar | editar a fonte]Os números complexos pódense identificar con puntos do plano euclidiano, é dicir, o número identifícase co punto . Baixo esta identificación, a circunferencia goniométrica trátase dun grupo coa operación de multiplicación, denominado grupo circular e usualmente denotado como 𝕋. Este grupo ten aplicacións moi importantes nas matemáticas e na ciencia.
Notas
[editar | editar a fonte]- ↑ Definicións no Dicionario da Real Academia Galega e no Portal das Palabras para goniometría.
- ↑ Weisstein, Eric W. "Unit Circle". mathworld.wolfram.com (en inglés). Consultado o 5 de maio de 2020.
- ↑ Weisstein, Eric W. "Hypersphere". mathworld.wolfram.com (en inglés). Consultado o 6 de maio de 2020.
Véxase tamén
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Circunferencia goniométrica |

























