Topoloxía
A topoloxía (do grego τοπος (topos) = lugar, e λογος (logos) = ciencia) é unha das máis importantes ramas da matemática moderna. Nun principio, a topoloxía investiga cal é a natureza do espazo (conxunto de puntos a estudar, dispostos dun xeito determinado), tanto dende un punto de vista global coma localmente, nunha veciñanza dun dos seus puntos.
A palabra topoloxía emprégase tanto para nomear á disciplina, como para referirse a calquera familia de conxuntos satisfacendo unhas determinadas propiedades e que son empregadas co fin de definir un espazo topolóxico concreto. Así pois, na topoloxía o espazo é formalizado a través da noción de espazo topolóxico. Esta estrutura matemática é a que permite falar de nocións espaciais relacionadas dalgún xeito coa proximidade de puntos, coma as de conexidade, continuidade, compacidade ou converxencia.
De especial importancia para a topoloxía é o estudo de determinadas funcións continuas definidas entre espazos topolóxicos, chamadas homeomorfismos, que intuitivamente establecen unha correspondencia global entre ámbolos dous espazos, indicando que o un pódese obter a partir do outro mediante determinadas deformacións que non inclúen nin cortes no espazo nin operacións de pegado.
Ramas da topoloxía
[editar | editar a fonte]
O concepto de espazo topolóxico xoga un papel fundamental na matemática actual, sendo unha noción unificadora que aparece en moi diversas ramas da matemática moderna. A topoloxía é en si mesma un amplo campo de estudo, que poderíase dividir dun xeito elemental en:
- Topoloxía xeral: estuda as propiedades de todo tipo de espazos topolóxicos e das estruturas neles definidas. Nocións coma as de compacidade e conexidade son estudadas neste campo da topoloxía.
- Topoloxía alxébrica: a través do emprego de certas ferramentas alxébricas investiga nocións coma as de homotopía e homoloxía en espazos topolóxicos.
- Topoloxía diferencial: estuda as propiedades topolóxicas dun tipo concreto de espazos topolóxicos, as variedades diferenciais.
Idea intuitiva
[editar | editar a fonte]
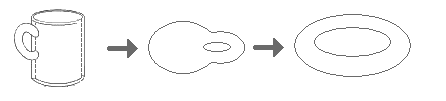
Na xeometría euclidiana dous obxectos serán equivalentes namentres poidamos transformar un no outro mediante isometrías (rotacións, translacións, reflexións etc), é dicir, mediante transformacións que conservan as medidas de ángulo, lonxitude, área, volume e outras. Na Topoloxía, dous obxectos son equivalentes nun sentido máis amplo. Han de ter o mesmo número de anacos, de buratos, de interseccións etc. Na topoloxía permítese dobrar, estirar, encoller, retorcer etc., os obxectos pero sempre que se faga sen romper nin separar o que estaba unido, nin pegar o que estaba separado. Por exemplo, un triángulo é topoloxicamente o mesmo que unha circunferencia, xa que podemos transformar o un na outra de forma continua, sen romper nin pegar. Pero unha circunferencia non é o mesmo que un segmento (xa que habería que partila por algún punto). Un chiste habitual entre os topólogos (os matemáticos que se dedican á topoloxía) di que «un topólogo é unha persoa incapaz de distinguir unha cunca dunha rosquilla». Pero esta visión, malia ser intuitiva e enxeñosa, é parcial. Por unha banda pode levar a pensar que a Topoloxía trata só de obxectos e conceptos xeométricos. Por outra banda, en moitos casos é imposible dar unha imaxe interpretativa dos problemas topolóxicos, ou incluso dalgúns conceptos.
Historia da topoloxía
[editar | editar a fonte]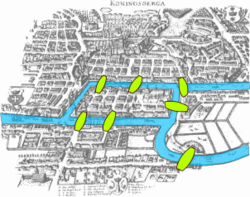
Habitualmente, a famosa cuestión acerca das sete pontes de Königsberg, sobre a imposibilidade de percorrer tódalas pontes desta cidade sen pasar dúas veces por ningunha delas, é considerada coma o primeiro problema de tipo topolóxico do que se ten constancia. Enténdese que é un problema de tipo topolóxico pois para a súa formulación abonda con achegar un plano esquemático coa disposición das pontes na cidade, sen importar as proporcións reais ou a forma exacta do río ou da cidade. Deste xeito, Leonhard Euler resolveu este problema no ano 1735 apoiándose na síntese do plano de Königsberg nun tipo de esquema chamado grafo (de aí que este problema sexa tamén citado a miúdo como a orixe da teoría de grafos).
Arredor do ano 1840, o matemático alemán Johann Benedict Listing (un dos descubridores da banda de Möbius) acuñou o termo topoloxía para designar a parte das matemáticas que Leibniz no 1679 chamara analysis situs, aínda cun sentido limitado de análise do lugar no que a posición viña totalmente relacionada coa distancia. Este termo foi o nome habitual da topoloxía ata comezos do século XX. Por exemplo, os conceptos de homotopía e homoloxía, básicos na topoloxía alxébrica actual foron introducidos no ano 1895 por Henri Poincaré no seu libro Analysis Situs.
Foi precisamente a necesidade de fundamentar as ideas de proximidade, veciñanza ou límite do cálculo infinitesimal desenvolto por Leibniz e Newton, ou o de variedade o que levou ó nacemento da topoloxía moderna a finais do século XIX e comezos do XX.
Como moitas outras ramas da matemática moderna, a topoloxía aséntase enormemente en nocións da teoría de conxuntos desenvolvidas por Georg Cantor a finais do século XIX, presentes, por exemplo, nos famosos axiomas que definen a noción de espazo topolóxico.
O termo espazo topolóxico foi introducido no ano 1914 por Felix Haussdorf para designar o que hoxe coñecemos como espazos Haussdorf, coa intención de xeneralizar a noción de espazo métrico introducida con anterioridade por Maurice Fréchet no 1906. A noción máis xeral de espazo topolóxico manexada na actualidade data do 1922 e débese a Kazimierz Kuratowski.
| Commons ten máis contidos multimedia sobre: Topoloxía |

