Función exponencial

A función exponencial é unha función matemática denotada por $f(x)=\exp(x)$ ou $e^{x}$ (onde o argumento $x$ escríbese coma un expoñente). A menos que se especifique o contrario, o termo refírese xeralmente á función con valores positivos dunha variábel real, aínda que se pode estender aos números complexos ou xeneralizarse a outros obxectos matemáticos como matrices ou álxebras de Lie. A función exponencial orixinouse da operación de tomar potencias dun número (multiplicación repetida), mais varias definicións modernas permiten estendela rigorosamente a todos os argumentos reais. $x$ , incluíndo números irracionais.

As funcións $f(x)=b^{x}$ para números reais positivos $b$ tamén se coñecen como funcións exponenciais e satisfán a identidade de exponenciación:

b^{x+y}=b^{x}b^{y}

para tódolos

x,y\in \mathbb {R} .

Isto implica $b^{n}=b\times \cdots \times b$ (con $n$ factores) para números enteiros positivos $n$ , onde $b=b^{1}$ , relacionando as funcións exponenciais coa noción elemental de exponenciación. A base natural $e=\exp(1)=2.71828\ldots$ é unha constante matemática ubicua chamada número de Euler. Para distinguilo, $\exp(x)=e^{x}$ chámase función exponencial ou función exponencial natural: é a única función con valor real dunha variábel real cuxa derivada é ela mesma e cuxo valor en $0$ é $1$ :

\exp '(x)=\exp(x)

para todos os

x\in \mathbb {R}

, e

\exp(0)=1.

A relación $b^{x}=e^{x\ln b}$ para $b>0$ e $x$ real ou complexa, permite expresar funcións exponenciais xerais en termos da exponencial natural.

De xeito máis xeral, calquera función $f:\mathbb {R} \to \mathbb {R}$ definida por

f(x)=ce^{ax}=cb^{kx},{\text{ con }}k=a/\ln b,\ a\neq 0,\ b,c>0

tamén se coñece como función exponencial, xa que resolve o problema do valor inicial $f'=af,\ f(0)=c$ , é dicir, a súa taxa de cambio en cada punto é proporcional ao valor da función nese punto. Este comportamento modela diversos fenómenos nas ciencias biolóxicas, físicas e sociais, por exemplo, o crecemento sen restricións dunha poboación que se reproduce por si mesmo, a desintegración dun elemento radioactivo, o interese composto que se acumula nun fondo financeiro ou a lei de Moore.

A función exponencial tamén se pode definir como unha serie de potencias, que se aplica facilmente a números reais, números complexos e mesmo matrices. A función exponencial complexa $\exp :\mathbb {C} \to \mathbb {C}$ toma todos os valores complexos agás 0 e está estreitamente relacionado coas funcións trigonométricas complexas pola fórmula de Euler:

$e^{x+iy}=e^{x}\cos(y)\,+\,i\,e^{x}\sin(y).$

A función exponencial dos números reais é unha bixección de $\mathbb {R}$ no intervalo $(0,\infty )$ .^[1] A súa función inversa é o logaritmo natural, denotado $\ln$ , $\log$ ou $\log _{e}$ .

Gráfica

A gráfica de $y=e^{x}$ ten pendente ascendente e aumenta máis rápido a medida que $x$ aumenta.^[2] A gráfica atópase sempre por riba do eixo $x$ , mais atópase arbitrariamente preto del para un $x$ negativo grande; así, o eixo $x$ é unha asíntota horizontal. A ecuación ${\tfrac {d}{dx}}e^{x}=e^{x}$ significa que a pendente da tanxente á gráfica en cada punto é igual á súa coordenada $y$ nese punto.

Definición formal

A función exponencial $\exp$ pode caracterizarse de diversas formas equivalentes. Normalmente defínese pola seguinte serie de potencias:^[3]^[4]

\exp x:=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots

Dado que o raio de converxencia desta serie de potencias é infinito, esta definición é aplicábel a todos os números complexos; ver plano complexo.

Resolvendo a ecuación diferencial ordinaria $y'(x)=y(x)$ coa condición inicial $y'(0)=1$ usando o método de Euler dá outra caracterización común, a fórmula do límite do produto: ^[4] $\exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}.$

Pódese demostrar que toda solución continua e distinta de cero da ecuación funcional $f(x+y)=f(x)f(y)$ para $f:\mathbb {C} \to \mathbb {C}$ é unha función exponencial no sentido máis xeral, $f(x)=\exp(kx)$ con $k\in \mathbb {C} .$

Derivadas e ecuacións diferenciais

A importancia da función exponencial en matemáticas e ciencias deriva principalmente da súa propiedade como función única que é igual á súa derivada e é igual a 1 cando $x = 0$ . É dicir, ${\frac {d}{dx}}e^{x}=e^{x},\quad e^{0}=1.$

As funcións da forma $ce x$ para a constante $c$ son as únicas funcións que son iguais á súa derivada (polo teorema de Picard–Lindelöf).

Tamén, para calquera función diferenciábel $f$ , atopamos, pola regra da cadea: ${\frac {d}{dx}}e^{f(x)}=f'(x)e^{f(x)}.$

Fraccións continuas para $e x$

Unha fracción continua para $e x$ pódese obter mediante unha identidade de Euler: $e^{x}=1+{\cfrac {x}{1-{\cfrac {x}{x+2-{\cfrac {2x}{x+3-{\cfrac {3x}{x+4-\ddots }}}}}}}}$

A seguinte fracción continua xeneralizada para $e z$ converxe máis rapidamente: $e^{z}=1+{\cfrac {2z}{2-z+{\cfrac {z^{2}}{6+{\cfrac {z^{2}}{10+{\cfrac {z^{2}}{14+\ddots }}}}}}}}$

Plano complexo

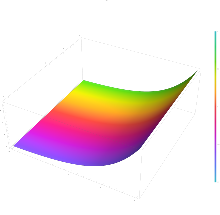
Como no caso real, a función exponencial pódese definir no plano complexo de varios xeitos equivalentes.

A definición máis común da función exponencial complexa é paralela á definición da serie de potencias para argumentos reais, onde a variábel real é substituída por outra complexa: $\exp z:=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}$

O mesmo pasa coa definición baseada no límite: $\exp z:=\lim _{n\to \infty }\left(1+{\frac {z}{n}}\right)^{n}$

Para a definición en serie de potencias, a multiplicación por termos de dúas copias desta serie de potencias no sentido de Cauchy, permitida polo teorema de Mertens, mostra que a propiedade multiplicativa definitoria das funcións exponenciais segue a ser válida para todos os argumentos complexos: $\exp(w+z)=\exp w\exp z{\text{ para todos os }}w,z\in \mathbb {C}$

A definición da función exponencial complexa leva á súa vez ás definicións adecuadas que estenden as funcións trigonométricas a argumentos complexos.

En particular, cando $z = it$ ( $t$ real), a definición da serie produce a expansión $\exp(it)=\left(1-{\frac {t^{2}}{2!}}+{\frac {t^{4}}{4!}}-{\frac {t^{6}}{6!}}+\cdots \right)+i\left(t-{\frac {t^{3}}{3!}}+{\frac {t^{5}}{5!}}-{\frac {t^{7}}{7!}}+\cdots \right).$

Nesta expansión, a reordenación dos termos en partes reais e imaxinarias está xustificada pola converxencia absoluta da serie. As partes real e imaxinaria da expresión anterior corresponden de feito ás expansións en serie de $cos t$ e $sin t$ , respectivamente.

Esta correspondencia proporciona un motivo para definir o coseno e o seno para todos os argumentos complexos en termos de $\exp(\pm iz)$ e a serie de potencias equivalentes: ${\begin{aligned}&\cos z:={\frac {\exp(iz)+\exp(-iz)}{2}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k}}{(2k)!}},\\[5pt]{\text{ e }}\quad &\sin z:={\frac {\exp(iz)-\exp(-iz)}{2i}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k+1}}{(2k+1)!}}\end{aligned}}$

para todo ${\textstyle z\in \mathbb {C} .}$

Estas definicións para as funcións exponenciais e trigonométricas conducen trivialmente á fórmula de Euler: $\exp(iz)=\cos z+i\sin z{\text{ for all }}z\in \mathbb {C} .$

A función exponencial complexa é periódica con período $2 πi$ e $\exp(z+2\pi ik)=\exp z$ cúmprese para todo $z\in \mathbb {C} ,k\in \mathbb {Z}$ .

Cando o seu dominio se estende desde a recta real ata o plano complexo, a función exponencial conserva as seguintes propiedades: ${\begin{aligned}&e^{z+w}=e^{z}e^{w},\\[5pt]&e^{0}=1,\\[5pt]&e^{z}\neq 0,\\[5pt]&{\frac {d}{dz}}e^{z}=e^{z},\\[5pt]&\left(e^{z}\right)^{n}=e^{nz},n\in \mathbb {Z} ,\end{aligned}}$

para todos os ${\textstyle w,z\in \mathbb {C} .}$

A extensión do logaritmo natural a argumentos complexos obtemos o logaritmo complexo $log z$ , que é unha función multivaluada.

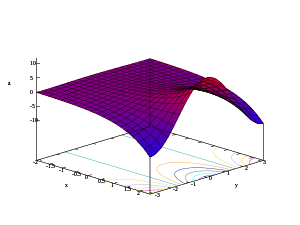
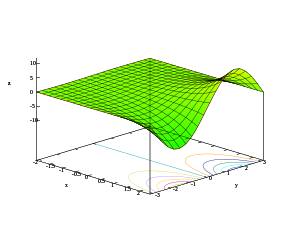
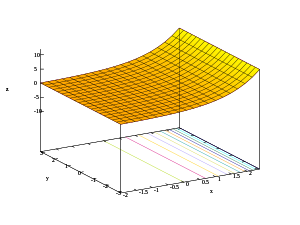
Gráficos 3D da parte real, parte imaxinaria e módulo da función exponencial
$z = Re(e x + iy)$
$z = Im(e x + iy)$
$z = | e x + iy |$

Cálculo de $a b$ onde tanto $a$ como $b$ son complexos

Artigo principal: Potenciación.

A exponenciación complexa $a b$ pódese definir convertendo $a$ en coordenadas polares e utilizando a identidade $(e ln a) b = a b$

a^{b}=\left(re^{\theta i}\right)^{b}=\left(e^{(\ln r)+\theta i}\right)^{b}=e^{\left((\ln r)+\theta i\right)b}

Cando $b$ non é un número enteiro, esta función ten varios valores, porque $θ$ non é único.

Álxebras de Lie

Dado un grupo de Lie $G$ e a súa álxebra de Lie asociada ${\mathfrak {g}}$ , o mapa exponencial é un mapa ${\mathfrak {g}}$ $\mapsto G$ que satisfai propiedades similares. De feito, dado que $R$ é a álxebra de Lie do grupo de Lie de todos os números reais positivos baixo multiplicación, a función exponencial ordinaria para argumentos reais é un caso especial da álxebra de Lie. Do mesmo xeito, dado que o grupo de Lie $GL(n, R)$ das matrices invertíbeis $n \times n$ ten como álxebra de Lie $M(n, R)$ , o espazo de todas as matrices $n \times n$ , a función exponencial para matrices cadradas é un caso especial do Mapa exponencial da álxebra de Lie.

A identidade $\exp(x+y)=\exp(x)\exp(y)$ pode fallar para os elementos da álxebra de Lie $x$ e $y$ que non conmuten; a fórmula de Baker–Campbell–Hausdorff proporciona os termos de corrección necesarios.

Transcendencia

A función $e z$ non está no anel das funcións racionais $\mathbb {C} (z)$ : non é o cociente de dous polinomios con coeficientes complexos.

Se $a 1, ..., a n$ son números complexos distintos, entón $e a 1 z, ..., e a n z$ son linearmente independentes sobre $\mathbb {C} (z)$ , e polo tanto $e z$ é transcendental en $\mathbb {C} (z)$ .

Notas

↑ Meier, John; Smith, Derek (7 August 2017). Exploring Mathematics. Cambridge University Press. p. 167. ISBN 978-1-107-12898-9.
↑ "Exponential Function Reference". www.mathsisfun.com. Consultado o 2020-08-28.
↑ Rudin, Walter (1987). Real and complex analysis (3rd ed.). New York: McGraw-Hill. p. 1. ISBN 978-0-07-054234-1.
↑ ^4,0 ^4,1 Weisstein, Eric W. "Exponential Function". mathworld.wolfram.com. Consultado o 2020-08-28.

Véxase tamén

Outros artigos

Lista de funcións matemáticas.

Ligazóns externas

"Exponential function". Encyclopedia of Mathematics. EMS Press. 2001 [1994].

[1] Meier, John; Smith, Derek (7 August 2017). Exploring Mathematics. Cambridge University Press. p. 167. ISBN 978-1-107-12898-9.

[2] "Exponential Function Reference". www.mathsisfun.com. Consultado o 2020-08-28.

[Rudin_1987-3] Rudin, Walter (1987). Real and complex analysis (3rd ed.). New York: McGraw-Hill. p. 1. ISBN 978-0-07-054234-1.

[:0-4] 4,0 ^4,1 Weisstein, Eric W. "Exponential Function". mathworld.wolfram.com. Consultado o 2020-08-28.

[1]

[2]

[3]

[4]