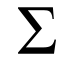En matemáticas , o sumatorio
(
∑
)
{\displaystyle {\Big (}\sum {\Big )}}
suma dunha secuencia de números , chamadas sumandos ; o resultado é a súa suma ou total .[ 1] funcións , vectores , matrices , polinomios e, en xeral, elementos de calquera tipo de obxectos matemáticos sobre os que se define unha operación denotada como "+".
Os sumatorios de secuencias infinitas chámanse series . Implican o concepto de límite , e non se consideran neste artigo.
Para sumas longas e sumatorios de lonxitude variable é un problema común atopar formas pechadas para o resultado. Por exemplo, [ a]
∑
i
=
1
n
i
=
n
(
n
+
1
)
2
.
{\displaystyle \sum _{i=1}^{n}i={\frac {n(n+1)}{2}}.}
O símbolo do sumatorio A notación matemática usa a letra grega grega maiúscula sigma para representar de forma compacta a suma de moitos termos similares, por exemplo:
∑
i
=
m
n
a
i
=
a
m
+
a
m
+
1
+
a
m
+
2
+
⋯
+
a
n
−
1
+
a
n
{\displaystyle \sum _{i\mathop {=} m}^{n}a_{i}=a_{m}+a_{m+1}+a_{m+2}+\cdots +a_{n-1}+a_{n}}
Onde i índice da suma ; ai m índice inferior da suma e n índice superior da suma . Por tanto no exemplo de enriba a suma irá desde o elemento número m ata o elmento número n indo o índice aumentando dun en un.[ b]
Isto lese como "suma de ai i m i n
Un exemplo que mostra a suma de algúns cadrados consecutivos:
∑
i
=
3
6
i
2
=
3
2
+
4
2
+
5
2
+
6
2
=
86.
{\displaystyle \sum _{i=3}^{6}i^{2}=3^{2}+4^{2}+5^{2}+6^{2}=86.}
E outro exemplo é a suma dos primeiros n secuencia de Fibonacci
∑
i
=
0
n
f
i
=
f
n
+
2
−
1.
{\displaystyle \sum _{i=0}^{n}f_{i}=f_{n+2}-1.}
Ás veces o índice e os límites dos índices do sumatorio omítense da definición do sumatorio se o contexto é suficientemente claro. Isto aplícase especialmente cando o índice vai de 1 a n .[ 2]
∑
a
i
2
=
∑
i
=
1
n
a
i
2
.
{\displaystyle \sum a_{i}^{2}=\sum _{i=1}^{n}a_{i}^{2}.}
Outro xeito é poñer a condición do índice toda no lado inferior, por exemplo:
∑
0
≤
k
<
100
f
(
k
)
{\displaystyle \sum _{0\leq k<100}f(k)}
Tamén se pode expresar como o percorrido polos elementos dun conxunto:
∑
x
∈
S
f
(
x
)
{\displaystyle \sum _{x\mathop {\in } S}f(x)}
f
(
x
)
{\displaystyle f(x)}
x
{\displaystyle x}
S
{\displaystyle S}
∑
d
|
n
μ
(
d
)
{\displaystyle \sum _{d\,|\,n}\;\mu (d)}
μ
(
d
)
{\displaystyle \mu (d)}
d
{\displaystyle d}
que dividen
n
{\displaystyle n}
Tamén hai formas de xeneralizar o uso de moitos signos sigma. Por exemplo,
∑
i
,
j
{\displaystyle \sum _{i,j}}
∑
i
∑
j
.
{\displaystyle \sum _{i}\sum _{j}.}
Unha notación similar úsase para o produto dunha secuencia, usando
∏
{\textstyle \prod }
pi .
Un sumatorio alterno de sumas e restas podemos definilo como:
∑
i
=
0
n
(
−
1
)
n
a
i
.
{\displaystyle \sum _{i=0}^{n}(-1)^{n}a_{i}.}
Dada unha función f que se define sobre os enteiros do intervalo [m , n ] , cúmprese a seguinte ecuación:
f
(
n
)
−
f
(
m
)
=
∑
i
=
m
n
−
1
(
f
(
i
+
1
)
−
f
(
i
)
)
.
{\displaystyle f(n)-f(m)=\sum _{i=m}^{n-1}(f(i+1)-f(i)).}
Esta coñécese como serie telescópica e é o análogo do teorema fundamental do cálculo no cálculo de diferenzas finitas , que afirma que:
f
(
n
)
−
f
(
m
)
=
∫
m
n
f
′
(
x
)
d
x
,
{\displaystyle f(n)-f(m)=\int _{m}^{n}f'(x)\,dx,}
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
derivada de f .Un exemplo de aplicación da ecuación anterior é o seguinte:
n
k
=
∑
i
=
0
n
−
1
(
(
i
+
1
)
k
−
i
k
)
.
{\displaystyle n^{k}=\sum _{i=0}^{n-1}\left((i+1)^{k}-i^{k}\right).}
Usando o teorema binomial , isto pódese reescribir como:
n
k
=
∑
i
=
0
n
−
1
(
∑
j
=
0
k
−
1
(
k
j
)
i
j
)
.
{\displaystyle n^{k}=\sum _{i=0}^{n-1}{\biggl (}\sum _{j=0}^{k-1}{\binom {k}{j}}i^{j}{\biggr )}.}
A fórmula anterior úsase máis habitualmente para inverter o operador diferenza
Δ
{\displaystyle \Delta }
Δ
(
f
)
(
n
)
=
f
(
n
+
1
)
−
f
(
n
)
,
{\displaystyle \Delta (f)(n)=f(n+1)-f(n),}
onde f é unha función definida nos enteiros non negativos. Así, dada tal función f , o problema é calcular a antidiferenza de f , unha función
F
=
Δ
−
1
f
{\displaystyle F=\Delta ^{-1}f}
Δ
F
=
f
{\displaystyle \Delta F=f}
F
(
n
+
1
)
−
F
(
n
)
=
f
(
n
)
.
{\displaystyle F(n+1)-F(n)=f(n).}
[ 3]
F
(
n
)
=
∑
i
=
0
n
−
1
f
(
i
)
.
{\displaystyle F(n)=\sum _{i=0}^{n-1}f(i).}
Non sempre hai unha expresión en forma pechada para tal suma, mais a fórmula de Faulhaber proporciona unha forma pechada no caso en que
f
(
n
)
=
n
k
{\displaystyle f(n)=n^{k}}
linearidade , para cada función polinómica de n .
Moitas aproximacións deste tipo pódense obter mediante a seguinte conexión entre sumas e integrais , que vale para calquera función crecente f :
∫
s
=
a
−
1
b
f
(
s
)
d
s
≤
∑
i
=
a
b
f
(
i
)
≤
∫
s
=
a
b
+
1
f
(
s
)
d
s
.
{\displaystyle \int _{s=a-1}^{b}f(s)\ ds\leq \sum _{i=a}^{b}f(i)\leq \int _{s=a}^{b+1}f(s)\ ds.}
e para calquera función decrecente f :
∫
s
=
a
b
+
1
f
(
s
)
d
s
≤
∑
i
=
a
b
f
(
i
)
≤
∫
s
=
a
−
1
b
f
(
s
)
d
s
.
{\displaystyle \int _{s=a}^{b+1}f(s)\ ds\leq \sum _{i=a}^{b}f(i)\leq \int _{s=a-1}^{b}f(s)\ ds.}
Para aproximacións máis xerais, consulte a fórmula de Euler-Maclaurin .
Para sumatorios nos que o sumando está dado (ou pode ser interpolado) por unha función integrable do índice, o sumatorio pode interpretarse como unha suma de Riemann que se produce na definición da integral definida correspondente. Polo tanto, pódese esperar que, por exemplo,
b
−
a
n
∑
i
=
0
n
−
1
f
(
a
+
i
b
−
a
n
)
≈
∫
a
b
f
(
x
)
d
x
,
{\displaystyle {\frac {b-a}{n}}\sum _{i=0}^{n-1}f\left(a+i{\frac {b-a}{n}}\right)\approx \int _{a}^{b}f(x)\ dx,}
xa que o lado dereito é por definición o límite para
n
→
∞
{\displaystyle n\to \infty }
n é fixo, non tende a infinito, e pouco se pode dicir sobre o erro na aproximación anterior sen presupostos adicionais sobre f : está claro que para funcións con oscilacións a grande escala a suma de Riemann pode estar arbitrariamente lonxe da integral de Riemann.
As fórmulas seguintes implican sumas finitas; para sumas infinitas ou sumas finitas de expresións que impliquen funcións trigonométricas ou outras funcións transcendentais , consulte a lista de series matemáticas .
∑
n
=
s
t
C
⋅
f
(
n
)
=
C
⋅
∑
n
=
s
t
f
(
n
)
{\displaystyle \sum _{n=s}^{t}C\cdot f(n)=C\cdot \sum _{n=s}^{t}f(n)\quad }
distributiva ).[ 4]
∑
n
=
s
t
f
(
n
)
±
∑
n
=
s
t
g
(
n
)
=
∑
n
=
s
t
(
f
(
n
)
±
g
(
n
)
)
{\displaystyle \sum _{n=s}^{t}f(n)\pm \sum _{n=s}^{t}g(n)=\sum _{n=s}^{t}\left(f(n)\pm g(n)\right)\quad }
conmutativa e asociativa ).[ 4]
∑
n
=
s
t
f
(
n
)
=
∑
n
=
s
+
p
t
+
p
f
(
n
−
p
)
{\displaystyle \sum _{n=s}^{t}f(n)=\sum _{n=s+p}^{t+p}f(n-p)\quad }
∑
n
∈
B
f
(
n
)
=
∑
m
∈
A
f
(
σ
(
m
)
)
,
{\displaystyle \sum _{n\in B}f(n)=\sum _{m\in A}f(\sigma (m)),\quad }
σ dun conxunto finito A nun conxunto B , mudar o índice, xeneraliza a fórmula precedente).
∑
n
=
s
t
f
(
n
)
=
∑
n
=
s
j
f
(
n
)
+
∑
n
=
j
+
1
t
f
(
n
)
{\displaystyle \sum _{n=s}^{t}f(n)=\sum _{n=s}^{j}f(n)+\sum _{n=j+1}^{t}f(n)\quad }
asociatividade ).
∑
n
=
a
b
f
(
n
)
=
∑
n
=
0
b
f
(
n
)
−
∑
n
=
0
a
−
1
f
(
n
)
{\displaystyle \sum _{n=a}^{b}f(n)=\sum _{n=0}^{b}f(n)-\sum _{n=0}^{a-1}f(n)\quad }
∑
n
=
s
t
f
(
n
)
=
∑
n
=
0
t
−
s
f
(
t
−
n
)
{\displaystyle \sum _{n=s}^{t}f(n)=\sum _{n=0}^{t-s}f(t-n)}
∑
n
=
0
t
f
(
n
)
=
∑
n
=
0
t
f
(
t
−
n
)
{\displaystyle \sum _{n=0}^{t}f(n)=\sum _{n=0}^{t}f(t-n)}
∑
i
=
k
0
k
1
∑
j
=
l
0
l
1
a
i
,
j
=
∑
j
=
l
0
l
1
∑
i
=
k
0
k
1
a
i
,
j
{\displaystyle \sum _{i=k_{0}}^{k_{1}}\sum _{j=l_{0}}^{l_{1}}a_{i,j}=\sum _{j=l_{0}}^{l_{1}}\sum _{i=k_{0}}^{k_{1}}a_{i,j}\quad }
∑
k
≤
j
≤
i
≤
n
a
i
,
j
=
∑
i
=
k
n
∑
j
=
k
i
a
i
,
j
=
∑
j
=
k
n
∑
i
=
j
n
a
i
,
j
=
∑
j
=
0
n
−
k
∑
i
=
k
n
−
j
a
i
+
j
,
i
{\displaystyle \sum _{k\leq j\leq i\leq n}a_{i,j}=\sum _{i=k}^{n}\sum _{j=k}^{i}a_{i,j}=\sum _{j=k}^{n}\sum _{i=j}^{n}a_{i,j}=\sum _{j=0}^{n-k}\sum _{i=k}^{n-j}a_{i+j,i}\quad }
∑
n
=
2
s
2
t
+
1
f
(
n
)
=
∑
n
=
s
t
f
(
2
n
)
+
∑
n
=
s
t
f
(
2
n
+
1
)
{\displaystyle \sum _{n=2s}^{2t+1}f(n)=\sum _{n=s}^{t}f(2n)+\sum _{n=s}^{t}f(2n+1)\quad }
∑
n
=
2
s
+
1
2
t
f
(
n
)
=
∑
n
=
s
+
1
t
f
(
2
n
)
+
∑
n
=
s
+
1
t
f
(
2
n
−
1
)
{\displaystyle \sum _{n=2s+1}^{2t}f(n)=\sum _{n=s+1}^{t}f(2n)+\sum _{n=s+1}^{t}f(2n-1)\quad }
(
∑
i
=
0
n
a
i
)
(
∑
j
=
0
n
b
j
)
=
∑
i
=
0
n
∑
j
=
0
n
a
i
b
j
{\displaystyle {\biggl (}\sum _{i=0}^{n}a_{i}{\biggr )}{\biggl (}\sum _{j=0}^{n}b_{j}{\biggr )}=\sum _{i=0}^{n}\sum _{j=0}^{n}a_{i}b_{j}\quad }
distributiva ).
∑
i
=
s
m
∑
j
=
t
n
a
i
c
j
=
(
∑
i
=
s
m
a
i
)
(
∑
j
=
t
n
c
j
)
{\displaystyle \sum _{i=s}^{m}\sum _{j=t}^{n}{a_{i}}{c_{j}}={\biggl (}\sum _{i=s}^{m}a_{i}{\biggr )}{\biggl (}\sum _{j=t}^{n}c_{j}{\biggr )}\quad }
∑
n
=
s
t
log
b
f
(
n
)
=
log
b
∏
n
=
s
t
f
(
n
)
{\displaystyle \sum _{n=s}^{t}\log _{b}f(n)=\log _{b}\prod _{n=s}^{t}f(n)}
C
∑
n
=
s
t
f
(
n
)
=
∏
n
=
s
t
C
f
(
n
)
{\displaystyle C^{\sum \limits _{n=s}^{t}f(n)}=\prod _{n=s}^{t}C^{f(n)}}
∑
m
=
0
k
∑
n
=
0
m
f
(
m
,
n
)
=
∑
m
=
0
k
∑
n
=
m
k
f
(
n
,
m
)
,
{\displaystyle \sum _{m=0}^{k}\sum _{n=0}^{m}f(m,n)=\sum _{m=0}^{k}\sum _{n=m}^{k}f(n,m),\quad }
f
{\textstyle f}
Z
×
Z
{\textstyle \mathbb {Z} \times \mathbb {Z} }
∑
i
=
1
n
c
=
n
c
{\displaystyle \sum _{i=1}^{n}c=nc\quad }
c que non depende de i .
∑
i
=
0
n
i
=
∑
i
=
1
n
i
=
n
(
n
+
1
)
2
{\displaystyle \sum _{i=0}^{n}i=\sum _{i=1}^{n}i={\frac {n(n+1)}{2}}}
[ 3]
∑
i
=
1
n
(
2
i
−
1
)
=
n
2
{\displaystyle \sum _{i=1}^{n}(2i-1)=n^{2}\qquad }
∑
i
=
0
n
2
i
=
n
(
n
+
1
)
{\displaystyle \sum _{i=0}^{n}2i=n(n+1)\qquad }
∑
i
=
1
n
log
i
=
log
n
!
{\displaystyle \sum _{i=1}^{n}\log i=\log n!\qquad }
logaritmos é o logaritmo do produto).
∑
i
=
0
n
i
2
=
∑
i
=
1
n
i
2
=
n
(
n
+
1
)
(
2
n
+
1
)
6
=
n
3
3
+
n
2
2
+
n
6
{\displaystyle \sum _{i=0}^{n}i^{2}=\sum _{i=1}^{n}i^{2}={\frac {n(n+1)(2n+1)}{6}}={\frac {n^{3}}{3}}+{\frac {n^{2}}{2}}+{\frac {n}{6}}}
[ 3]
∑
i
=
0
n
i
3
=
(
∑
i
=
0
n
i
)
2
=
(
n
(
n
+
1
)
2
)
2
=
n
4
4
+
n
3
2
+
n
2
4
{\displaystyle \sum _{i=0}^{n}i^{3}={\biggl (}\sum _{i=0}^{n}i{\biggr )}^{2}=\left({\frac {n(n+1)}{2}}\right)^{2}={\frac {n^{4}}{4}}+{\frac {n^{3}}{2}}+{\frac {n^{2}}{4}}\qquad }
Teorema de Nicómaco ) [ 3] Nos seguintes sumatorios, asúmese que a é diferente de 1.
∑
i
=
0
n
−
1
a
i
=
1
−
a
n
1
−
a
{\displaystyle \sum _{i=0}^{n-1}a^{i}={\frac {1-a^{n}}{1-a}}}
progresión xeométrica ).
∑
i
=
0
n
−
1
1
2
i
=
2
−
1
2
n
−
1
{\displaystyle \sum _{i=0}^{n-1}{\frac {1}{2^{i}}}=2-{\frac {1}{2^{n-1}}}}
a = 1/2
∑
i
=
0
n
−
1
i
a
i
=
a
−
n
a
n
+
(
n
−
1
)
a
n
+
1
(
1
−
a
)
2
{\displaystyle \sum _{i=0}^{n-1}ia^{i}={\frac {a-na^{n}+(n-1)a^{n+1}}{(1-a)^{2}}}}
a veces a derivada en relación a a da progresión xeométrica).
∑
i
=
0
n
−
1
(
b
+
i
d
)
a
i
=
b
∑
i
=
0
n
−
1
a
i
+
d
∑
i
=
0
n
−
1
i
a
i
=
b
(
1
−
a
n
1
−
a
)
+
d
(
a
−
n
a
n
+
(
n
−
1
)
a
n
+
1
(
1
−
a
)
2
)
=
b
(
1
−
a
n
)
−
(
n
−
1
)
d
a
n
1
−
a
+
d
a
(
1
−
a
n
−
1
)
(
1
−
a
)
2
{\displaystyle {\begin{aligned}\sum _{i=0}^{n-1}\left(b+id\right)a^{i}&=b\sum _{i=0}^{n-1}a^{i}+d\sum _{i=0}^{n-1}ia^{i}\\&=b\left({\frac {1-a^{n}}{1-a}}\right)+d\left({\frac {a-na^{n}+(n-1)a^{n+1}}{(1-a)^{2}}}\right)\\&={\frac {b(1-a^{n})-(n-1)da^{n}}{1-a}}+{\frac {da(1-a^{n-1})}{(1-a)^{2}}}\end{aligned}}}
(suma dunha secuencia aritmético-xeométrica ) Existen moitas identidades con sumatorios que implican coeficientes binomiais. Algunhas das máis básicas son as seguintes.
∑
i
=
0
n
(
n
i
)
a
n
−
i
b
i
=
(
a
+
b
)
n
,
{\displaystyle \sum _{i=0}^{n}{n \choose i}a^{n-i}b^{i}=(a+b)^{n},}
teorema do binomio .
∑
i
=
0
n
(
n
i
)
=
2
n
,
{\displaystyle \sum _{i=0}^{n}{n \choose i}=2^{n},}
a = b = 1
∑
i
=
0
n
(
n
i
)
p
i
(
1
−
p
)
n
−
i
=
1
{\displaystyle \sum _{i=0}^{n}{n \choose i}p^{i}(1-p)^{n-i}=1}
p = a = 1 − b
0
≤
p
≤
1
,
{\displaystyle 0\leq p\leq 1,}
distribución binomial .
∑
i
=
0
n
i
(
n
i
)
=
n
(
2
n
−
1
)
,
{\displaystyle \sum _{i=0}^{n}i{n \choose i}=n(2^{n-1}),}
a = b = 1derivada con respecto a a do teorema do binomio.
∑
i
=
0
n
(
n
i
)
i
+
1
=
2
n
+
1
−
1
n
+
1
,
{\displaystyle \sum _{i=0}^{n}{\frac {n \choose i}{i+1}}={\frac {2^{n+1}-1}{n+1}},}
a = b = 1a do teorema do binomio.Nos seguintes sumatorios,
n
P
k
{\displaystyle {}_{n}P_{k}}
k n
∑
i
=
0
n
i
P
k
(
n
i
)
=
n
P
k
(
2
n
−
k
)
{\displaystyle \sum _{i=0}^{n}{}_{i}P_{k}{n \choose i}={}_{n}P_{k}(2^{n-k})}
∑
i
=
1
n
i
+
k
P
k
+
1
=
∑
i
=
1
n
∏
j
=
0
k
(
i
+
j
)
=
(
n
+
k
+
1
)
!
(
n
−
1
)
!
(
k
+
2
)
{\displaystyle \sum _{i=1}^{n}{}_{i+k}P_{k+1}=\sum _{i=1}^{n}\prod _{j=0}^{k}(i+j)={\frac {(n+k+1)!}{(n-1)!(k+2)}}}
∑
i
=
0
n
i
!
⋅
(
n
i
)
=
∑
i
=
0
n
n
P
i
=
⌊
n
!
⋅
e
⌋
,
n
∈
Z
+
{\displaystyle \sum _{i=0}^{n}i!\cdot {n \choose i}=\sum _{i=0}^{n}{}_{n}P_{i}=\lfloor n!\cdot e\rfloor ,\quad n\in \mathbb {Z} ^{+}}
⌊
x
⌋
{\displaystyle \lfloor x\rfloor }
función chan .
∑
k
=
0
m
(
n
+
k
n
)
=
(
n
+
m
+
1
n
+
1
)
{\displaystyle \sum _{k=0}^{m}{\binom {n+k}{n}}={\binom {n+m+1}{n+1}}}
∑
i
=
k
n
(
i
k
)
=
(
n
+
1
k
+
1
)
{\displaystyle \sum _{i=k}^{n}{i \choose k}={n+1 \choose k+1}}
∑
i
=
0
n
i
⋅
i
!
=
(
n
+
1
)
!
−
1
{\displaystyle \sum _{i=0}^{n}i\cdot i!=(n+1)!-1}
∑
i
=
0
n
(
m
+
i
−
1
i
)
=
(
m
+
n
n
)
{\displaystyle \sum _{i=0}^{n}{m+i-1 \choose i}={m+n \choose n}}
∑
i
=
0
n
(
n
i
)
2
=
(
2
n
n
)
{\displaystyle \sum _{i=0}^{n}{n \choose i}^{2}={2n \choose n}}
∑
i
=
0
n
1
i
!
=
⌊
n
!
e
⌋
n
!
{\displaystyle \sum _{i=0}^{n}{\frac {1}{i!}}={\frac {\lfloor n!\;e\rfloor }{n!}}}
∑
i
=
1
n
1
i
=
H
n
{\displaystyle \sum _{i=1}^{n}{\frac {1}{i}}=H_{n}\quad }
n -ésimo número harmónico )
∑
i
=
1
n
1
i
k
=
H
n
k
{\displaystyle \sum _{i=1}^{n}{\frac {1}{i^{k}}}=H_{n}^{k}\quad }
número harmónico xeneralizado )
↑ "Sumatorio" . aplicacions.usc.es; bUSCatermos . Consultado o 2023-09-15 . ↑ "sumatorio" . www.columbia.edu . ↑ 3,0 3,1 3,2 3,3 Handbook of Discrete and Combinatorial Mathematics , Kenneth H. Rosen, John G. Michaels, CRC Press, 1999, ISBN 0-8493-0149-1 .↑ 4,0 4,1 "notación sumatorio" . tutorial.math.lamar.edu .
↑ Para máis detalles, ver Número triangular .
↑ Para unha exposición detallada da notación do sumatorio e aritmética con sumas, ver Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994). "Chapter 2: Sums". Concrete Mathematics: A Foundation for Computer Science (2nd ed.). Addison-Wesley Professional. ISBN 978-0201558029 .