Leis de De Morgan

En lóxica proposicional e álxebra de Boole, as leis de De Morgan,^[1]^[2]^[3] tamén coñecidas como teorema de De Morgan,^[4] son un par de regras de transformación que son regras de inferencia válidas. Levan o nome de Augustus De Morgan, un matemático británico do século XIX. As regras permiten a expresión de conxuncións e disxuncións unicamente en termos entre si mediante a negación.

As regras pódense expresar en texto como:

A negación de "A e B" é o mesmo que "non A ou non B".
A negación de "A ou B" é o mesmo que "non A e non B".

ou

O complementario da unión de dous conxuntos é o mesmo que a intersección dos seus complementos
O complementario da intersección de dous conxuntos é o mesmo que a unión dos seus complementarios

ou

non (A ou B) = (non A) e (non B)
non (A e B) = (non A) ou (non B)

onde "A ou B" é "ou inclusivo" que significa polo menos un de A ou B en lugar de "ou exclusivo" que significa exactamente un de A ou B.

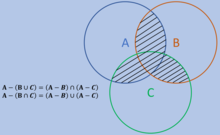
Outra forma da lei de De Morgan é a seguinte como se ve a continuación.

A-(B\cup C)=(A-B)\cap (A-C),

A-(B\cap C)=(A-B)\cup (A-C).

A aplicación destas regras inclúen a simplificación de expresións lóxicas en programas informáticos e deseños de circuítos dixitais. As leis de De Morgan son un exemplo dun concepto máis xeral de dualidade matemática.

Notación formal

A regra de negación da conxunción pódese escribir en notación de consecuentes:

{\begin{aligned}\neg (P\land Q)&\vdash (\neg P\lor \neg Q).\\(\neg P\lor \neg Q)&\vdash \neg (P\land Q).\end{aligned}}

A regra de negación da disxunción pódese escribir como:

{\begin{aligned}\neg (P\lor Q)&\vdash (\neg P\land \neg Q).\\(\neg P\land \neg Q)&\vdash \neg (P\lor Q).\end{aligned}}

En forma de regra: negación da conxunción

${\frac {\neg (P\land Q)}{\therefore \neg P\lor \neg Q}}\qquad {\frac {\neg P\lor \neg Q}{\therefore \neg (P\land Q)}}$

e negación da disxunción

${\frac {\neg (P\lor Q)}{\therefore \neg P\land \neg Q}}\qquad {\frac {\neg P\land \neg Q}{\therefore \neg (P\lor Q)}}$

e exprésase como tautoloxías ou teoremas de lóxica proposicional de funcións de verdade:

{\begin{aligned}\neg (P\land Q)&\leftrightarrow (\neg P\lor \neg Q),\\\neg (P\lor Q)&\leftrightarrow (\neg P\land \neg Q).\\\end{aligned}}

onde $P$ e $Q$ son proposicións expresadas nalgún sistema formal.

As leis xeneralizadas de De Morgan proporcionan unha equivalencia para negar unha conxunción ou disxunción que implica varios termos.Para un conxunto de proposicións $P_{1},P_{2},\dots ,P_{n}$ , as leis de De Morgan xeneralizadas son as seguintes:

{\begin{aligned}\lnot (P_{1}\land P_{2}\land \dots \land P_{n})\leftrightarrow \lnot P_{1}\lor \lnot P_{2}\lor \ldots \lor \lnot P_{n}\\\lnot (P_{1}\lor P_{2}\lor \dots \lor P_{n})\leftrightarrow \lnot P_{1}\land \lnot P_{2}\land \ldots \land \lnot P_{n}\end{aligned}}

Forma de substitución

As leis de De Morgan móstranse normalmente na forma compacta anterior, coa negación da saída á esquerda e a negación das entradas á dereita. Unha forma máis clara para a substitución pódese indicar como:

{\begin{aligned}(P\land Q)&\Longleftrightarrow \neg (\neg P\lor \neg Q),\\(P\lor Q)&\Longleftrightarrow \neg (\neg P\land \neg Q).\end{aligned}}

Isto fai fincapé na necesidade de inverter tanto as entradas como a saída, así como mudar o operador ao facer unha substitución.

Teoría de conxuntos

Na teoría de conxuntos, adoita dicirse como "troco de unión e intersección baixo complementación",^[5] que se pode expresar formalmente como:

{\begin{aligned}{\overline {A\cup B}}&={\overline {A}}\cap {\overline {B}},\\{\overline {A\cap B}}&={\overline {A}}\cup {\overline {B}},\end{aligned}}

onde:

${\overline {A}}$ é a negación de $A$ , escribindo a liña superior enriba dos termos que se van negar,
$\cap$ é o operador de intersección (AND),
$\cup$ é o operador únión (OR).

Álxebra de Boole

Na álxebra de Boole, do mesmo xeito, esta lei pode expresarse formalmente como:

{\begin{aligned}{\overline {A\land B}}&={\overline {A}}\lor {\overline {B}},\\{\overline {A\lor B}}&={\overline {A}}\land {\overline {B}},\end{aligned}}

onde:

${\overline {A}}$ é a negación de $A$ , escribindo a liña superior enriba dos termos que se van negar,
$\land$ é o operador de conxunción lóxica (AND),
$\lor$ é o operador de disxunción lóxica (OR).

Enxeñaría

En enxeñaría eléctrica e informática, as leis de De Morgan escríbense habitualmente como:

{\overline {(A\cdot B)}}\equiv ({\overline {A}}+{\overline {B}})

{\overline {(A+B)}}\equiv ({\overline {A}}\cdot {\overline {B}}),

onde:

$\cdot$ é o AND lóxico,
$+$ é o OR lóxico,
a liña superior é o NOT lóxico do que hai debaixo da barra superior.

Busca de texto (informática)

As leis de De Morgan adoitan aplicarse á busca de texto mediante operadores booleanos AND, OR e NOT. Considere un conxunto de documentos que conteñan as palabras "gatos" e "cans". As leis de De Morgan sosteñen que estas dúas procuras devolverán o mesmo conxunto de documentos:

Busca A: NON (gatos OU cans)

Busca B: (NON gatos) E (NON cans)

Pódese aplicar unha avaliación similar para mostrar que as dúas buscas seguintes:

Busca C: NOT (gatos E cans),

Busca D: (NON gatos) OU (NON cans).

Notas

↑ Copi, Irving M.; Cohen, Carl; McMahon, Kenneth (2016). Introduction to Logic. ISBN 9781315510880. doi:10.4324/9781315510897.
↑ Hurley, Patrick J. (2015). A Concise Introduction to Logic (12th ed.). Cengage Learning. ISBN 978-1-285-19654-1.
↑ Moore, Brooke Noel (2012). Critical thinking. Richard Parker (10th ed.). New York: McGraw-Hill. ISBN 978-0-07-803828-0. OCLC 689858599.
↑ DeMorgan's [sic] Theorem
↑ Boolean Algebra by R. L. Goodstein. ISBN 0-486-45894-6

Véxase tamén

Bibliografía

Outros artigos

Táboa de verdade.

Ligazóns externas

"Duality principle". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
Weisstein, Eric W. "de Morgan's Laws". MathWorld.
de Morgan's laws at PlanetMath.
Duality in Logic and Language, Internet Encyclopedia of Philosophy.

[1] Copi, Irving M.; Cohen, Carl; McMahon, Kenneth (2016). Introduction to Logic. ISBN 9781315510880. doi:10.4324/9781315510897.

[2] Hurley, Patrick J. (2015). A Concise Introduction to Logic (12th ed.). Cengage Learning. ISBN 978-1-285-19654-1.

[3] Moore, Brooke Noel (2012). Critical thinking. Richard Parker (10th ed.). New York: McGraw-Hill. ISBN 978-0-07-803828-0. OCLC 689858599.

[4] DeMorgan's [sic] Theorem

[r_l_goodstein-5] Boolean Algebra by R. L. Goodstein. ISBN 0-486-45894-6

[1]

[2]

[3]

[4]

[5]