Matriz de adxacencia

En teoría de grafos e informática, unha matriz de adxacencia é unha matriz cadrada usada para representar un grafo finito. Os elementos da matriz indican se os pares de vértices son adxacentes ou non no grafo.

No caso especial dun grafo simple finito, a matriz de adxacencia é unha matriz (0,1) con ceros na súa diagonal. Se o grafo é non orientado (é dicir, todas as súas arestas son bidireccionais), a matriz de adxacencia é simétrica.

A relación entre un grafo e os autovalores e vectores propios da súa matriz de adxacencia estúdase na teoría espectral de grafos.

A matriz de adxacencia dun grafo debe distinguirse da súa matriz de incidencia, unha representación matricial diferente cuxos elementos indican se os pares vértice-aresta son incidentes ou non, e a súa matriz de graos, que contén información sobre o grao de cada vértice.

Definición

Para un grafo simple co conxunto de vértices $U = {u 1, ..., u n}$ , a matriz de adxacencia é unha matriz $A$ cadrada $n \times n$ tal que o seu elemento $A ij$ é 1 cando hai unha aresta desde o vértice $u i$ ata o vértice $u j$ , e 0 cando non hai aresta.

Os elementos diagonais da matriz son todos 0, xa que os bordos dun vértice ata si mesmo ( bucles ) non están permitidos nos grafos simples.

O mesmo concepto pódese estender a multigrafos e grafos con bucles almacenando o número de arestas entre cada dous vértices no elemento correspondente da matriz e permitindo elementos diagonais distintos de cero.

Os bucles pódense contar unha vez (como unha única aresta) ou dúas veces (como dúas incidencias de arestas de vértice), sempre que se siga unha convención consistente.

Os grafos non orientados adoitan usar a última convención de contar bucles dúas veces, mentres que os grafos orientados normalmente usan a primeira convención.

A matriz de distancias ten na posición $(i, j)$ a distancia entre os vértices $v i$ e $v j$ . A distancia é a lonxitude do camiño máis curto que une os vértices. A información que proporciona en lugar de dicir só se dous vértices están ligados ou non (é dicir, a matriz de conexión, que contén valores booleanos), dá a distancia exacta entre eles.

Exemplos

Grafos non orientados

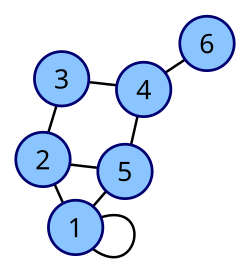
A convención seguida aquí (para grafos non orientados) é que cada aresta engade 1 á cela apropiada da matriz e cada bucle (unha aresa desde un vértice ata si mesmo) engade 2 á cela apropiada na diagonal da matriz. Isto permite atopar facilmente o grao dun vértice tomando a suma dos valores na súa fila ou columna respectiva na matriz de adxacencia.

Grafo etiquetado	Matriz de adxacencia
	${\begin{pmatrix}2&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\end{pmatrix}}$ As coordenadas son 1-6.
Grafo de Nauru	As coordenadas son 0-23. Os campos brancos son ceros, os de cores son uns.

Grafos orientados

A matriz de adxacencia dun grafo orientado pode ser asimétrica. Pódese definir a matriz de adxacencia dun grafo orientado de xeito que

un elemento distinto de cero $A ij$ indica unha aresta de $i$ a $j$ ou
indica unha aresta de $j$ a $i$ .

A primeira definición úsase habitualmente na teoría de grafos e na análise de redes sociais (por exemplo, socioloxía, ciencias políticas, economía, psicoloxía).

A segunda definición é máis común noutras ciencias aplicadas (por exemplo, sistemas dinámicos, física, ciencia de redes) onde $A$ ás veces úsase para describir dinámica linear en grafos.

Usando a primeira definición, o grao de entrada dun vértice pódese calcular sumando as entradas da columna correspondente e o grao de saída do vértice sumando as entradas da fila correspondente.

Grafo etiquetado	Matriz de adxacencia
Grafo de Cayley orientado de S₄	As coordenadas son 0-23. Como o grafo está orientado, a matriz non é necesariamente simétrica.

Propiedades

Espectro

A matriz de adxacencia dun grafo simple non orientado é simétrica e, polo tanto, ten un conxunto completo de valores propios reais e unha base de vectores propios ortogonal.

O conxunto de valores propios dun grafo é o espectro do grafo.^[1] É común denotar os autovalores por $\lambda _{1}\geq \lambda _{2}\geq \cdots \geq \lambda _{n}.$

O maior valor propio $\lambda _{1}$ está limitada por riba polo grao máximo. Isto pódese ver como o resultado do teorema de Perron-Frobenius, mais pódese probar facilmente.

Sexa $v$ un vector propio asociado a $\lambda _{1}$ e $x$ a entrada na que $v$ ten o valor absoluto máximo. Sen perda de xeneralidade supoña que $v x$ é positivo xa que se non, simplemente tomamos o vector propio $-v$ , tamén asociado a $\lambda _{1}$ . Daquela

\lambda _{1}v_{x}=(Av)_{x}=\sum _{y=1}^{n}A_{x,y}v_{y}\leq \sum _{y=1}^{n}A_{x,y}v_{x}=v_{x}\deg(x).

Para grafos $d$ -regulares, $d$ é o primeiro autovalor de $A$ para o vector $v = (1, ..., 1)$ (é doado comprobar que é un autovalor e é o máximo debido ao límite anterior).

A multiplicidade deste autovalor é o número de compoñentes conectados de $G$ , en particular $\lambda _{1}>\lambda _{2}$ para grafos conexos.

Pódese demostrar que para todo valor propio $\lambda _{i}$ , o seu oposto $-\lambda _{i}=\lambda _{n+1-i}$ tamén é un valor propio de $A$ se $G$ é un grafo bipartito. En particular − $d$ é un valor propio de calquera grafo bipartito $d$ -regular.

A diferenza $\lambda _{1}-\lambda _{2}$ chámase fenda espectral e está relacionada coa expansión de $G$ . Tamén é útil introducir o raio espectral de $A$ denotado como $\lambda (G)=\max _{\left|\lambda _{i}\right|<d}|\lambda _{i}|$ .

Este número está limitado por $\lambda (G)\geq 2{\sqrt {d-1}}-o(1)$ . Este límite é axustado nos grafos de Ramanujan.

Isomorfismo e invariantes

Supoña que se dan dous grafos orientados ou non orientados $G 1$ e $G 2$ con matrices de adxacencia $A 1$ e $A 2$ . $G 1$ e $G 2$ son isomorfos se e só se existe unha matriz de permutación $P$ tal que

PA_{1}P^{-1}=A_{2}.

En particular, $A 1$ e $A 2$ son semellantes e polo tanto teñen o mesmo polinomio mínimo, polinomio característico, valores propios, determinante e traza.

Polo tanto, eses valores e ecuacións poden servir como invariantes de isomorfismo dos grafos. No entanto, dous grafos poden posuír o mesmo conxunto de valores propios mais non ser isomorfos. Eses operadores lineares dise que son isoespectrais.

Potencias da matriz

Se $A$ é a matriz de adxacencia do grafo orientado ou non $G$ , entón a matriz $A n$ (é dicir, o produto matricial de $n$ copias de $A$ ) ten unha interpretación interesante: o elemento $(i, j)$ dá o número de camiños (orientados ou non) de lonxitude $n$ dende o vértice $i$ ata o vértice $j$ .

Se $n$ é o número enteiro non negativo máis pequeno, de xeito que para algúns $i$ , $j$ , o elemento $(i, j)$ de $A n$ é positivo, entón $n$ é a distancia entre o vértice $i$ e o vértice $j$ .

Un gran exemplo de como isto é útil é contar o número de triángulos nun grafo non orientado $G$ , que é exactamente a traza de $A 3$ dividido por 3 ou 6 dependendo de se o grafo está orientado ou non. Dividimos por eses valores para compensar a sobrecontaxe de cada triángulo.

Nun grafo non orientado, cada triángulo contarase dúas veces para os tres nós, porque o camiño pódese seguir no sentido horario ou antihorario: ijk ou ikj.

A matriz de adxacencia pódese usar para determinar se o grafo é conexo ou non.

Se un grafo orientado ten unha matriz de adxacencia nilpotente (é dicir, se existe $n$ tal que $A n$ é a matriz cero), entón é un grafo acíclico orientado.^[2]

Notas

↑ Biggs (1993), Chapter 2 ("The spectrum of a graph"), pp. 7–13.
↑ Nicholson, Victor A (1975). "Matrices with Permanent Equal to One" (PDF). Linear Algebra and Its Applications (12): 187.

Véxase tamén

Outros artigos

Ligazóns externas

Weisstein, Eric W. "Adjacency matrix". MathWorld.
Fluffschack — an educational Java web start game demonstrating the relationship between adjacency matrices and graphs.
Open Data Structures - Section 12.1 - AdjacencyMatrix: Representing a Graph by a Matrix, Pat Morin
Café math : Adjacency Matrices of Graphs : Application of the adjacency matrices to the computation generating series of walks.

[1] Biggs (1993), Chapter 2 ("The spectrum of a graph"), pp. 7–13.

[2] Nicholson, Victor A (1975). "Matrices with Permanent Equal to One" (PDF). Linear Algebra and Its Applications (12): 187.

[1]

[2]