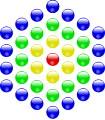
Número figurado

Derivado do Triángulo de Pascal xustificado á esquerda .      Número natural      Número triangular      Número tetrahédrico      Número Pentatópico      Número 5-simplex      Número 6-simplex      Número 7-simplex

En aritmética, un número figurado é un número enteiro que se pode representar por un conxunto de puntos dispostos máis ou menos regularmente e formando unha figura xeométrica. Polo tanto, responde a unha clase particular de problemas de contaxe.

Os números figurados son de orixe moi antiga. Xeralmente atribúense a Pitágoras os primeiros estudos dos números figurados .

Exemplo de números figurados

Os números figurados máis sinxelos son

• Números cadrados

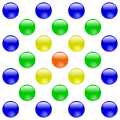
1	4	9

• Números triangulares

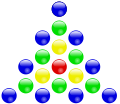
1	3	6

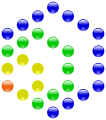
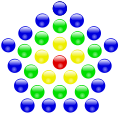
• Números hexagonais centrados

1	7	19

Corresponden, por exemplo, á distribución dos conos de cor no centro da retina, ou á dos alvéolos das abellas.

• Números cúbicos :

1, 8, 27, 64

que debuxan un cubo no espazo.

Rutas de exploración

O primeiro contacto que todo ser pensante ten co número é a través do número figurado. É unha linguaxe universal non ligada á escritura e aos sistemas de numeración. O número figurado permite demostrar que certos animais (o polbo por exemplo) teñen conciencia do número. En pedagoxía, pasar polo figurado permítenos visualizar propiedades como a conmutatividade ou asociatividade leis de suma e multiplicación (leis que se ditan construíndo filas ou táboas de puntos). A relación 2 + 3 = 3 + 2 = 5, por exemplo, que reflicte o feito de que 2 e 3 son permutábeis para a suma, pódese representar por

+ = + =

E a relación 2 × 3 = 3 × 2 = 6 (que reflicte o feito de que 2 e 3 son permutables para a multiplicación) pódese representar por

2 × 3	3 × 2	6

O estudo dos números figurados consiste xeralmente en atopar unha relación entre o propio número e a súa posición na serie. Por exemplo, o número triangular de posición n é n ( n + 1)/2. O número cúbico de posición n é n 3 . Os conceptos de números figurados implican implícitamente o concepto "moderno» de recorrencia.

Unha segunda vía de investigación é determinar as propiedades dos números que aparecen na mesma serie. Por exemplo, é fácil demostrar que non hai números primos entre os números triangulares (agás 3), cadrados ou rectángulos.

Outra vía de investigación é utilizar os números figurados para resolver ecuacións en ℕ como a extracción da raíz cadrada e raíz cúbica.

Clasificación

Os números figurados están dispostos segundo a dimensión da figura representada. En dimensións superiores ou iguais a 4, os números figurados xa non poden representarse mediante figuras correspondentes ao mundo tanxíbel senón que se consideran vistas da mente. A figura é entón un polítopo e o número chámase entón número polítopo.

Na dimensión 1

Os números lineares son os enteiros clásicos.

Na dimensión 2

• Números poligonais (triangulares, cadrados, pentagonais, hexagonais, heptagonais, octogonais ou gnomónicos).

• 
  10 é un número triangular
• 
  16 é un número cadrado
• 
  Números pentagonais 5,12, 22, 35
• 
  28 é un número hexagonal

• Números poligonais centrados (triangulares, cadrados, pentagonais, hexagonais, heptagonais, octogonais).

• 
  19 é un número triangular centrado
• 
  25 é un número cadrado centrado
• 
  31 é un número pentagonal centrado
• 
  37 é un número hexagonal centrado

Na dimensión 3

Números cúbicos

• Números piramidais (tetraédrico, cadrado piramidal, pentagonal piramidal, hexagonal piramidal)
• Números poliédricos (tetraédrico, cúbico, octaédrico, dodecaédrico, icosaédrico )
• Números poliédricos centrados (tetraédrico, cúbico, octaédrico, dodecaédrico, icosaédrico)

Na dimensión 4

• Números pentatópicos, pentacóricos ou 4-hipertetraédricos
• Números pentatópicos centrados o pentacóricos centrados, ou números 4 hipertetraédricos centrados

• Os números 4-hipercúbicos, 4-hiperoctaédricos, 4-hiperdodecaédricos, 4-hipericosaédricos]

Véxase tamén

Outros artigos

• Número triangular.
• Teorema de Pick