Terna pitagórica

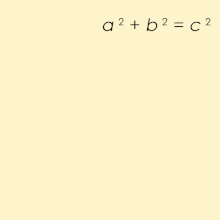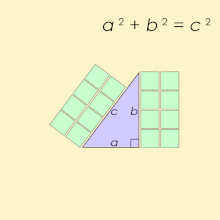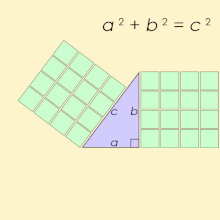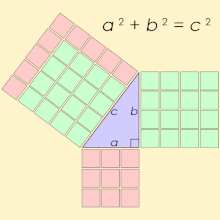
Unha terna pitagórica consta de tres números enteiros positivos $a$ , $b$ e $c$ , de tal forma que $a 2 + b 2 = c 2$ . Tal terna escríbese habitualmente $(a, b, c)$ , un exemplo coñecido é $(3, 4, 5)$ . Se $(a, b, c)$ é unha terna pitagórica, entón tamén o é $(ka, kb, kc)$ para calquera número enteiro positivo $k$ . Un triángulo cuxos lados son unha terna pitagórica é un triángulo rectángulo e chámase triángulo pitagórico.

Unha terna pitagórica primitiva é aquela na que $a$ , $b$ e $c$ son coprimos (é dicir, non teñen un divisor común maior que 1).^[1] Por exemplo, $(3, 4, 5)$ é unha terna pitagórica primitiva mentres que $(6, 8, 10)$ non o é.

Procurar solucións enteiras da ecuación $a 2 + b 2 = c 2$ é unha ecuación diofantiana. Así, as ternas pitagóricas están entre as solucións máis antigas coñecidas dunha ecuación diofantiana non linear.

Exemplos

Hai 16 ternas pitagóricas primitivas de números por debaixo de 100:

(3, 4, 5)	(5, 12, 13)	(8, 15, 17)	(7, 24, 25)
(20, 21, 29)	(12, 35, 37)	(9, 40, 41)	(28, 45, 53)
(11, 60, 61)	(16, 63, 65)	(33, 56, 65)	(48, 55, 73)
(13, 84, 85)	(36, 77, 85)	(39, 80, 89)	(65, 72, 97)

Xerando unha terna

Artigo principal: Fórmulas para xerar ternas pitagóricas.

A fórmula de Euclides é unha fórmula fundamental para xerar ternas pitagóricas dado un par arbitrario de números enteiros $m$ e $n$ con $m > n > 0$ . A fórmula indica que os números enteiros

a=m^{2}-n^{2},\ \,b=2mn,\ \,c=m^{2}+n^{2}

forman unha terna pitagórica. Por exemplo, dado

m=9,\ \,n=2

xera a terna primitiva (36,77,85):

b=9^{2}-2^{2}=77,\ \,a=2\times 9\times 2=36,\ \,c=9^{2}+2^{2}=85.

A terna xerada pola fórmula de Euclides é primitiva se e só se $m$ e $n$ son coprimos e exactamente un deles é par.^[2]

Malia xerar todas as ternas primitivas, a fórmula de Euclides non produce todas as ternas; por exemplo, (9, 12, 15) non se pode xerar usando os números enteiros $m$ e $n$ . Pódense conseguir todas incluíndo un parámetro:

a=k\cdot (m^{2}-n^{2}),\ \,b=k\cdot (2mn),\ \,c=k\cdot (m^{2}+n^{2})

Escoller $m$ e $n$ entre certas secuencias enteiras dá resultados interesantes. Por exemplo, se $m$ e $n$ son números de Pell consecutivos, $a$ e $b$ diferirán en 1.

x={\frac {1-t^{2}}{1+t^{2}}}\quad y={\frac {2t}{1+t^{2}}}.

P=\left({\frac {2\left({\frac {m}{n}}\right)}{\left({\frac {m}{n}}\right)^{2}+1}},{\frac {\left({\frac {m}{n}}\right)^{2}-1}{\left({\frac {m}{n}}\right)^{2}+1}}\right)=\left({\frac {2mn}{m^{2}+n^{2}}},{\frac {m^{2}-n^{2}}{m^{2}+n^{2}}}\right).

Propiedades elementais das ternas pitagóricas primitivas

As propiedades dunha terna pitagórica primitiva $(a, b, c)$ con $a < b < c$ (sen especificar cal de $a$ ou $b$ é par e cal é impar) inclúen:

${\tfrac {(c-a)(c-b)}{2}}$ é sempre un cadrado perfecto.^[3]

Como moito un entre $a$ , $b$ e $c$ é un cadrado.^[4]
A area dun triángulo pitagórico non pode ser un cadrado nen dúas veces un cadrado dun enteiro^[5]^{:p. 17} ^[5]^{:p. 21}.
Exactamente un de $a$ ou $b$ é divisible por 2 (é par), e a hipotenusa $c$ é sempre impar.^[6]
Exactamente un de $a$ ou $b$ é divisible por 3, mais nunca $c$ .^[7]^[6]^:23–25
Exactamente un de $a$ ou $b$ é divisible por 4, mais nunca $c$ .^[6]
Exactamente un de $a$ , $b$ ou $c$ é divisible por 5.^[6]
Calquera número impar da forma $2 m +1$ , onde $m$ é un número enteiro e $m >1$ , pode ser a pata impar dunha terna pitagórica primitiva. Porén, só os números pares divisibles por 4 poden ser o cateto par dunha terna pitagórica primitiva. Isto débese a que a fórmula de Euclides para o cateto par dada enriba é $2 mn$ e unha de entre $m$ ou $n$ debe ser igual.
A hipotenusa $c$ (que é sempre impar) é a suma de dous cadrados. Isto require que os seus factores sexan todos da forma $4k+1$ . Por tanto, c é da forma $4 k + 1$ . A secuencia de números posibles da hipotenusa pode verse en (secuencia A008846 na OEIS).
A área $(K = ab /2)$ é un número divisible por 6.

Non hai triángulos pitagóricos nos que a hipotenusa e un cateto sexan catetos doutro triángulo pitagórico; esta é unha das formas equivalentes do teorema do triángulo rectángulo de Fermat.^[5]^:p.14
Cada triángulo pitagórico primitivo ten unha proporción de área, $K$ , a semiperímetro cadrado, $s$ , que é única para si e vén dada por^[8]

{\frac {K}{s^{2}}}={\frac {n(m-n)}{m(m+n)}}=1-{\frac {c}{s}}.

Ningún triángulo pitagórico primitivo ten unha altitude enteira a partir da hipotenusa. ^[9]
Ningún dos ángulos agudos dun triángulo pitagórico pode ser un número racional en graos^[10],(isto ven dado polo teorema de Niven.)

Xeometría da fórmula de Euclides

Puntos racionais na circunferencia unitaria

A fórmula de Euclides para unha terna pitagórica

a=m^{2}-n^{2},\quad b=2mn,\quad c=m^{2}+n^{2}

pódese entender en termos da xeometría dos puntos racionais na círcunferencia unitaria (Trautman 1998).

De feito, un punto do plano cartesiano con coordenadas $(x, y)$ pertence á circunferencia unitaria se $x 2 + y 2 = 1$ . O punto é racional se $x$ e $y$ son números racionais, é dicir, se hai coprimos enteiros $a, b, c$ tal que

{\biggl (}{\frac {a}{c}}{\biggr )}^{2}+{\biggl (}{\frac {b}{c}}{\biggr )}^{2}=1.

Ao multiplicar os dous membros por $c 2$ , pódese ver que os puntos racionais da circunferencia están en correspondencia un a un coas ternas pitagóricas primitivas.

O circunferencia unitaria tamén se pode definir mediante unha ecuación paramétrica

x={\frac {1-t^{2}}{1+t^{2}}}\quad y={\frac {2t}{1+t^{2}}}.

A fórmula de Euclides para as ternas pitagóricas e a relación inversa $t = y / (x + 1)$ significan que, agás para $(-1 , 0)$ , un punto $(x, y)$ na circunferencia é racional se e só se o valor correspondente de $t$ é un número racional. Teña en conta que $t = y / (x + 1) = b / (a + c) = n / m$ tamén é a tanxente da metade do ángulo que está oposto ao lado do triángulo de lonxitude $b$ .

Aproximación estereográfica

Proxección estereográfica da circunferencia unitaria sobre o eixo $x$ . Dado un punto $P$ na circunferencia unitaria, traza unha recta dende $P$ ata o punto $N = (0, 1)$ (*polo norte*). O punto $P$ ′ onde a recta corta co eixo $x$ é a proxección estereográfica de $P$ . Inversamente, comezando cun punto $P$ ′ no eixo $x$ , e trazando unha liña de $P$ ′ a $N$ , a proxección estereográfica inversa é o punto $P$ onde a recta corta a circunferencia unitaria.

Hai unha correspondencia entre os puntos da circunferencia unitaria con coordenadas racionais e as ternas pitagóricas primitivas. Neste punto, as fórmulas de Euclides pódense derivar mediante métodos de trigonometría ou de forma equivalente usando a proxección estereográfica.

Para o enfoque estereográfico, supoña que $P$ ′ é un punto no eixo $x$ con coordenadas racionais

$P'=\left({\frac {m}{n}},0\right).$

Daquela, pódese demostrar mediante álxebra básica que o punto $P$ ten coordenadas

\left({\frac {x}{1-y}},0\right)

que é racional.

En termos de xeometría alxébrica, a variedade alxébrica de puntos racionais na circunferencia unitaria é biracional á recta afín sobre os números racionais. A circunferencia unitaria chámase así unha curva racional, e é este feito o que permite unha parametrización explícita dos puntos (número racional) sobre ela por medio de funcións racionais.

Espinors e o grupo modular

As ternas pitagóricas tamén se poden codificar nunha matriz cadrada da forma

X={\begin{bmatrix}c+b&a\\a&c-b\end{bmatrix}}.

Unha matriz desta forma é simétrica con determinante

\det X=c^{2}-a^{2}-b^{2}\,

que é cero precisamente cando $(a, b, c)$ é unha terna pitagórica. Se $X$ corresponde a unha terna pitagórica, entón como matriz debe ter rango 1.

Dado que $X$ é simétrico, dun resultado en álxebra linear dedúcese que hai un vector columna $ξ = [m n] T$ tal que o produto externo

X=2{\begin{bmatrix}m\\n\end{bmatrix}}[m\ n]=2\xi \xi ^{T}\,

(1)

cúmprese. Dado que ξ e -ξ producen a mesma terna pitagórica, o vector ξ pódese considerar un espinor (para o grupo de Lorentz SO(1, 2)). En termos abstractos, a fórmula de Euclides significa que cada terna pitagórica primitiva pode escribirse como o produto exterior consigo mesmo dun espinor con entradas enteiras, como en (1).

O grupo modular Γ é o conxunto de matrices 2×2 con coeficientes enteiros

A={\begin{bmatrix}\alpha &\beta \\\gamma &\delta \end{bmatrix}}

con determinante igual a un: $αδ - βγ = 1$ . O grupo modular actúa sobre a colección de todos os espinors enteiros. Ademais, o grupo é transitivo na colección de espinors enteiros con entradas coprimas. Pois se $[m n] T$ ten coeficientes coprimos, entón

{\begin{bmatrix}m&-v\\n&u\end{bmatrix}}{\begin{bmatrix}1\\0\end{bmatrix}}={\begin{bmatrix}m\\n\end{bmatrix}}

onde se seleccionan $u$ e $v$ (mediante o algoritmo de Euclides) para que cumpran $mu + nv = 1$ .

Ao actuar sobre o espinor ξ en (1), a acción de Γ pasa a ser unha acción sobre as ternas pitagóricas, sempre que se permitan ternas con compoñentes posiblemente negativas. Así, se $A$ é unha matriz en $Γ$ , entón

2(A\xi )(A\xi )^{T}=AXA^{T}\,

(2)

dá lugar a unha acción sobre a matriz $X$ en (1).

Alternativamente, podemos restrinxir a acción a aqueles valores de $m$ e $n$ para os que $m$ é impar e $n$ é par. Sexa o subgrupo Γ(2) de Γ o kernel do homomorfismo de grupo

\Gamma =\mathrm {SL} (2,\mathbf {Z} )\to \mathrm {SL} (2,\mathbf {Z} _{2})

onde $SL(2, Z 2)$ é o grupo linear especial sobre o corpo finito $Z 2$ de enteiros módulo 2. Entón Γ(2) é o grupo de transformacións unimodulares que conservan a paridade de cada entrada. Así, se a primeira entrada de ξ é impar e a segunda é par, entón o mesmo ocorre con $A ξ$ para todo $A \in Γ(2)$ . De feito, baixo a acción (2), o grupo Γ(2) actúa transitivamente sobre a colección das ternas pitagóricas primitivas (Alperin 2005).

Así temos que o grupo Γ(2) é o grupo libre cuxos xeradores son as matrices

U={\begin{bmatrix}1&2\\0&1\end{bmatrix}},\qquad L={\begin{bmatrix}1&0\\2&1\end{bmatrix}}.

En consecuencia, cada terna pitagórica primitiva pode obterse dun xeito único como produto das copias das matrices $U$ e $L$ .

Relación cos enteiros gaussianos

Se consideramos o cadrado dun número enteiro gaussiano, obtemos a seguinte interpretación directa da fórmula de Euclides como a representación dun cadrado perfecto dun enteiro gaussiano.

(m+ni)^{2}=(m^{2}-n^{2})+2mni.

Usando os feitos de que os enteiros gaussianos son un dominio euclidiano e que para un enteiro gaussiano p, $|p|^{2}$ é sempre un cadrado, é posible demostrar que unha terna pitagórica corresponde ao cadrado dun primo enteiro gaussiano se a hipotenusa é un número primo.

Se o número enteiro gaussiano non é primo, entón é o produto de dous enteiros gaussianos p e q con $|p|^{2}$ e $|q|^{2}$ enteiros. Dado que as magnitudes se multiplican nos enteiros gaussianos, o produto debe ser $|p||q|$ , que cando se eleva ao cadrado para atopar unha terna pitagórica debe ser composto. O contrapositivo completa a proba.

Ecuacións relacionadas

Ecuación de Jacobi–Madden

a^{4}+b^{4}+c^{4}+d^{4}=(a+b+c+d)^{4}

é equivalente á terna especial Pitagórica,

(a^{2}+ab+b^{2})^{2}+(c^{2}+cd+d^{2})^{2}=((a+b)^{2}+(a+b)(c+d)+(c+d)^{2})^{2}

Hai un número infinito de solucións a esta ecuación xa que a resolución das variables implica unha curva elíptica. Algunhas solucións pequenas,

a,b,c,d=-2634,955,1770,5400

a,b,c,d=-31764,7590,27385,48150

Sumas iguais de dous cadrados

Un xeito de xerar solucións a $a^{2}+b^{2}=c^{2}+d^{2}$ é parametrizar a, b, c, d en termos de enteiros m, n, p, q como segue:^[11]

(m^{2}+n^{2})(p^{2}+q^{2})=(mp-nq)^{2}+(np+mq)^{2}=(mp+nq)^{2}+(np-mq)^{2}.

Teorema do círculo de Descartes

Para o caso do Teorema do círculo de Descartes onde todas as variables son cadrados,

2(a^{4}+b^{4}+c^{4}+d^{4})=(a^{2}+b^{2}+c^{2}+d^{2})^{2}

Euler demostrou que isto é equivalente a tres ternas pitagóricas simultáneas,

(2ab)^{2}+(2cd)^{2}=(a^{2}+b^{2}-c^{2}-d^{2})^{2}

(2ac)^{2}+(2bd)^{2}=(a^{2}-b^{2}+c^{2}-d^{2})^{2}

(2ad)^{2}+(2bc)^{2}=(a^{2}-b^{2}-c^{2}+d^{2})^{2}

Tamén hai un número infinito de solucións, e para o caso especial cando $a+b=c$ , a ecuación simplifícase a:

4(a^{2}+ab+b^{2})=d^{2}

con solucións pequenas como $a,b,c,d=3,5,8,14$ e pódense resolver como formas cadráticas binarias.

Ternas do triángulo de Herón

Artigo principal: triángulo de Herón.

Un triángulo de Herón defínese habitualmente como aquel con lados enteiros cuxa área tamén é un número enteiro. As lonxitudes dos lados deste triángulo forman unha terna de Herón $(a, b, c)$ con $a \leq b \leq c$ . Toda terna pitagórica é unha terna de Herón, porque na terna pitagórica polo menos un dos catetos $a$ , $b$ debe ser par, polo que a área ab/2 é un número enteiro. Non toda terna de Herón é unha terna pitagórica, como mostra o exemplo $(4, 13, 15)$ de área 24.

Se $(a, b, c)$ é unha terna de Herón, tamén o é $(ka, kb, kc)$ onde $k$ é calquera número enteiro positivo; a súa área será o número enteiro que é $k 2$ veces a área enteira do triángulo $(a, b, c)$ . A terna de Herón $(a, b, c)$ é primitiva cando a, b, ' 'c son coprimos en conxunto,(non é necesario que sexan coprimos por parellas). Aquí vemos algunhas das ternas de Herón primitivas máis simples que non son ternas pitagóricas:

(4, 13, 15) con área 24

(3, 25, 26) con área 36

(7, 15, 20) con área 42

(6, 25, 29) con área 60

(11, 13, 20) con área 66

Pola fórmula de Herón, a condición adicional para que unha terna de números enteiros positivos $(a, b, c)$ con $a < b < c$ sexa terna de Herón é que

(a 2 + b 2 + c 2) 2 - 2(a 4 + b 4 + c 4)

ou equivalentemente

2(a 2 b 2 + a 2 c 2 + b 2 c 2) - (a 4 + b 4 + c 4)

sexa un cadrado perfecto distinto de cero divisíbel por 16.

Notas

↑ Long (1972)
↑ Mitchell, Douglas W. (July 2001). An Alternative Characterisation of All Primitive Pythagorean Triples. The Mathematical Gazette 85. pp. 273–5. JSTOR 3622017. doi:10.2307/3622017.
↑ Posamentier, Alfred S. (2010). The Pythagorean Theorem: The Story of Its Power and Beauty. Prometheus Books. p. 156. ISBN 9781616141813. .
↑ Para a non existencia de solucións cando $a$ and $b$ son ambos os dous cadrados, orixinalmente probado por Fermat, ver Koshy, Thomas (2002). Elementary Number Theory with Applications. Academic Press. p. 545. ISBN 9780124211711. .
↑ ^5,0 ^5,1 ^5,2 Carmichael, Robert D. (1915). Diophantine Analysis. John Wiley & Sons.
↑ ^6,0 ^6,1 ^6,2 ^6,3 Sierpiński, Wacław (2003). Pythagorean Triangles. Dover. ISBN 978-0-486-43278-6.
↑ Proceedings of the Southeastern Conference on Combinatorics, Graph Theory, and Computing, Volume 20. Utilitas Mathematica Pub. 1990. p. 141. ISBN 9780919628700.
↑ Rosenberg, Steven; Spillane, Michael; Wulf, Daniel B. (May 2008). Heron triangles and moduli spaces. Mathematics Teacher 101. pp. 656–663. doi:10.5951/MT.101.9.0656.
↑ Yiu, Paul (2008). Heron triangles which cannot be decomposed into two integer right triangles (PDF). 41st Meeting of Florida Section of Mathematical Association of America. p. 17. Arquivado dende o orixinal (PDF) o 02 de maio de 2013. Consultado o 20 de abril de 2024.
↑ Weisstein, Eric W., "Rational Triangle", MathWorld
↑ Nahin, Paul J. (1998). An Imaginary Tale: The Story of sqrt{-1}. Princeton, New Jersey: Princeton University Press. pp. 25–26. ISBN 0-691-02795-1. MR 1645703.

Véxase tamén

Bibliografía

Alperin, Roger C. (2005). The modular tree of Pythagoras (PDF). American Mathematical Monthly 112. pp. 807–816. JSTOR 30037602. MR 2179860. doi:10.2307/30037602.
Berggren, B. (1934). Pytagoreiska trianglar. Tidskrift för Elementär Matematik, Fysik och Kemi (en sueco) 17. pp. 129–139.
Barning, F.J.M. (1963). Over pythagorese en bijna-pythagorese driehoeken en een generatieproces met behulp van unimodulaire matrices (PDF). Math. Centrum Amsterdam Afd. Zuivere Wisk. (en neerlandés). ZW-011. p. 37.
Eckert, Ernest (1992). Primitive Pythagorean triples. The College Mathematics Journal 23. pp. 413–417. JSTOR 2686417. doi:10.2307/2686417.
Elkies, Noam. Pythagorean triples and Hilbert's theorem 90 (PDF).
Heath, Thomas (1956). The Thirteen Books of Euclid's Elements Vol. 1 (Books I and II) (2nd ed.). Dover Publications. ISBN 978-0-486-60088-8.
Long, Calvin T. (1972). Elementary Introduction to Number Theory (2nd ed.). Lexington: D. C. Heath and Company. LCCN 77171950.
Martin, Artemas (1875). Rational right angled triangles nearly isosceles. The Analyst 3. pp. 47–50. JSTOR 2635906. doi:10.2307/2635906.
McCullough, Darryl (2005). Height and excess of Pythagorean triples (PDF). Mathematics Magazine 78. pp. 26–44. doi:10.1080/0025570X.2005.11953298.
Romik, Dan (2008). The dynamics of Pythagorean triples (PDF). Trans. Amer. Math. Soc. 360. pp. 6045–6064. MR 2425702. arXiv:math.DS/0406512. doi:10.1090/S0002-9947-08-04467-X.
Teigen, M.G.; Hadwin, D.W. (1971). On Generating Pythagorean Triples. The American Mathematical Monthly 78. pp. 378–379. JSTOR 2316903. doi:10.2307/2316903.
Trautman, Andrzej (1998). "Pythagorean spinors and Penrose twistors". En S.A. Hugget; L.J. Mason; K.P. Tod; S.T. Tsou; N.M.J. Woodhouse. Geometric universe (Postscript).

Outros artigos

Ligazóns externas

Clifford Algebras and Euclid's Parameterization of Pythagorean triples
Curious Consequences of a Miscopied Quadratic
Discussion of Properties of Pythagorean triples, Interactive Calculators, Puzzles and Problems
Generating Pythagorean Triples Using Arithmetic Progressions
"Pythagorean numbers". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
Interactive Calculator for Pythagorean Triples
The negative Pell equation and Pythagorean triples
Parameterization of Pythagorean Triples by a single triple of polynomials
Price, H. Lee (2008), The Pythagorean Tree: A New Species, arXiv:0809.4324
Pythagorean Triples and the Unit Circle, chap. 2–3, in "A Friendly Introduction to Number Theory" by Joseph H. Silverman, 3rd ed., 2006, Pearson Prentice Hall, Upper Saddle River, NJ, ISBN 0-13-186137-9
Pythagorean Triples at cut-the-knot Interactive Applet showing unit circle relationships to Pythagorean Triples
Pythagorean Triplets
The Remarkable Incircle of a Triangle
Solutions to Quadratic Compatible Pairs in relation to Pythagorean Triples
Theoretical properties of the Pythagorean Triples and connections to geometry
The Trinary Tree(s) underlying Primitive Pythagorean Triples at cut-the-knot
Weisstein, Eric W., "Pythagorean Triple", MathWorld

[1] Long (1972)

[2] Mitchell, Douglas W. (July 2001). An Alternative Characterisation of All Primitive Pythagorean Triples. The Mathematical Gazette 85. pp. 273–5. JSTOR 3622017. doi:10.2307/3622017.

[3] Posamentier, Alfred S. (2010). The Pythagorean Theorem: The Story of Its Power and Beauty. Prometheus Books. p. 156. ISBN 9781616141813. .

[4] Para a non existencia de solucións cando $a$ and $b$ son ambos os dous cadrados, orixinalmente probado por Fermat, ver Koshy, Thomas (2002). Elementary Number Theory with Applications. Academic Press. p. 545. ISBN 9780124211711. .

[Carmichael1-5] 5,0 ^5,1 ^5,2 Carmichael, Robert D. (1915). Diophantine Analysis. John Wiley & Sons.

[Sierpinski-6] 6,0 ^6,1 ^6,2 ^6,3 Sierpiński, Wacław (2003). Pythagorean Triangles. Dover. ISBN 978-0-486-43278-6.

[7] Proceedings of the Southeastern Conference on Combinatorics, Graph Theory, and Computing, Volume 20. Utilitas Mathematica Pub. 1990. p. 141. ISBN 9780919628700.

[8] Rosenberg, Steven; Spillane, Michael; Wulf, Daniel B. (May 2008). Heron triangles and moduli spaces. Mathematics Teacher 101. pp. 656–663. doi:10.5951/MT.101.9.0656.

[Yiu-9] Yiu, Paul (2008). Heron triangles which cannot be decomposed into two integer right triangles (PDF). 41st Meeting of Florida Section of Mathematical Association of America. p. 17. Arquivado dende o orixinal (PDF) o 02 de maio de 2013. Consultado o 20 de abril de 2024.

[10] Weisstein, Eric W., "Rational Triangle", MathWorld

[11] Nahin, Paul J. (1998). An Imaginary Tale: The Story of sqrt{-1}. Princeton, New Jersey: Princeton University Press. pp. 25–26. ISBN 0-691-02795-1. MR 1645703.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]