Monoide

En álxebra abstracta, unha rama das matemáticas, un monoide é un conxunto equipado cunha operación binaria asociativa e un elemento identidade. Por exemplo, os enteiros non negativos con suma forman un monoide, sendo o elemento de identidade $0$ .

Os monoides son semigrupos con identidade.

As funcións dun conxunto forman un monoide con respecto á composición de funcións. De forma máis xeral, na teoría de categorías, os morfismos dun obxecto en si mesmo forman un monoide e, por outra parte, un monoide pode ser visto como unha categoría cun só obxecto.

Definición

Un conxunto $S$ equipado cunha operación binaria $S \times S \to S$ , que denotaremos $•$ , é un monoide se cumpre os dous axiomas seguintes:

Asociatividade: Para todos os $a$ , $b$ e $c$ en $S$ , cúmprese a ecuación $(a • b) • c = a • (b • c)$ .
Elemento identidade: Existe un elemento $e$ en $S$ tal que para cada elemento $a$ en $S$ , cúmprense as igualdades $e • a = a$ e $a • e = a$ .

Noutras palabras, un monoide é un semigrupo cun elemento identidade. Tamén se pode pensar como un magma con asociatividade e identidade. O elemento identidade dun monoide é único.^[a] Por esta razón, a identidade considérase como unha constante, é dicir, operación $0$ -aria (ou nula). O monoide, polo tanto, caracterízase pola especificación do tupla $(S, •, e)$ .

Un monoide no que cada elemento ten unha inversa é un grupo.

Un monoide cuxa operación é conmutativa chámase monoide conmutativo (ou, con menos frecuencia, monoide abeliano).

Propiedades

Os axiomas do monoide implican que o elemento identidade $e$ é único: Se $e$ e $f$ son elementos de identidade dun monoide, entón $e = ef = f$ .

Elementos invertíbeis

Un elemento $x$ chámase invertíbel se existe un elemento $y$ tal que $x • y = e$ $y • x = e$ . O elemento $y$ chámase inverso de $x$ . Os inversos, se os existen, son únicos: se $y$ e $z$ son inversos de $x$ , entón por asociatividade $y = ey = (zx) y = z (xy) = ze = z$ . ^[1]

Se $x$ é invertíbel, digamos con inverso $y$ , entón pódense definir potencias negativas de $x$ estabelecendo $x - n = y n$ para cada $n \geq 1$ ; isto fai que a ecuación $x m + n = x m • x n$ se cumpra para todo $m, n \in Z$ .

O conxunto de todos os elementos invertíbeis dun monoide, xunto coa operación •, forma un grupo.

Grupo de Grothendieck

Non todos os monoides encaixan dentro dun grupo.

Un monoide $(M, •)$ ten a propiedade de cancelación (é cancelativo) se para todo $a$ , $b$ e $c$ en $M$ , a igualdade $a • b = a • c$ implica $b = c$ , e a igualdade $b • a = c • a$ implica $b = c$ .

Un monoide conmutativo coa propiedade de cancelación sempre se pode mergullar nun grupo mediante a construción de grupo de Grothendieck. Así é como se constrúe o grupo aditivo dos enteiros (un grupo con operación $+$ ) a partir do monoide aditivo dos números naturais (un monoide conmutativo con operación $+$ e propiedade de cancelación).

Se un monoide ten a propiedade de cancelación e é finito, entón é de feito un grupo.^[b]

A propiedade cancelativa nun monoide non é necesaria para realizar a construción de Grothendieck: a conmutatividade é suficiente. Porén, se un monoide conmutativo non ten a propiedade de cancelación, o homomorfismo do monoide no seu grupo de Grothendieck non é inxectivo. Máis precisamente, se $a • b = a • c$ , entón $b$ e $c$ teñen a mesma imaxe no grupo de Grothendieck, aínda que $b \neq c$ . En particular, se o monoide ten un elemento absorbente, entón o seu grupo de Grothendieck é o grupo trivial.

Monoide inverso

Un monoide inverso é un monoide onde para todo $a$ en $M$ , existe un único $a -1$ en $M$ tal que $a = a • a -1 • a$ e $a -1 = a -1 • a • a -1$ . Se un monoide inverso é cancelativo, daqula é un grupo.

Homomorfismos de monoides

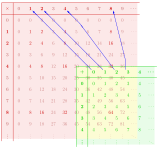
Un homomorfismo entre dous monoides $(M, *)$ e $(N, •)$ é unha función $f : M \to N$ tal que

$f (x * y) = f (x) • f (y)$ para todo $x$ , $y$ en $M$
$f (e M) = e N$ ,

onde $e M$ e $e N$ son as identidades en $M$ e $N$ respectivamente. Os homomorfismos monoides ás veces chámanse simplemente morfismos monoides.

Non todos os homomorfismos de semigrupos entre monoides son homomorfismos de monoides, xa que poden non mapear a identidade coa identidade do monoide obxectivo, aínda que a identidade sexa a identidade da imaxe do homomorfismo.^[c] Por exemplo, considere $[Z] n$ , o conxunto de clases de residuos módulo $n$ equipadas coa multiplicación. En particular, $[1] n$ é o elemento de identidade. A función $f : [Z] 3 \to [Z] 6$ dada por $[k] 3 \mapsto [3 k] 6$ é un homomorfismo de semigrupo, xa que $[3 k \cdot 3 l] 6 = [9 kl] 6 = [3 kl] 6$ . Porén, $f ([1] 3) = [3] 6 \neq [1] 6$ , polo que un homomorfismo monoide é un homomorfismo de semigrupos entre monoides que mapea a identidade do primeiro monoide coa identidade do segundo monoide e a última condición non pode ser omitida.

En contraste, un homomorfismo de semigrupos entre grupos é sempre un homomorfismo de grupos, xa que necesariamente preserva a identidade (porque, no grupo obxectivo do homomorfismo, o elemento identidade é o único elemento $x$ tal que $x \cdot x = x$ ).

Un homomorfismo de monoides bixectivo chámase isomorfismo de monoides. Dous monoides dise que son isomorfos se hai un isomorfismo de monoides entre eles.

Notas

↑ Jacobson 2009, p. 31.

↑ Se ambos os dous $e 1$ e $e 2$ satisfán as ecuacións, daquela $e 1 = e 1 • e 2 = e 2$ .
↑ Proba: Fixamos un elemento $x$ do monoide. Dado que o monoide é finito, $x n = x m$ para algún $m > n > 0$ . Mais daquela, debido á cancelación temos que $x m - n = e$ onde $e$ é a identidade. Por tanto, $x • x m - n -1 = e$ , e así $x$ ten inversa.
↑ $f (x) * f (e M) = f (x * e M) = f (x)$ para todo $x$ en $M$ , cando $f$ é un homomorfismo de semigrupos e $e M$ é a identidade do dominio do seu monoide $M$ .

Véxase tamén

Bibliografía

Jacobson, Nathan (1951). Lectures in Abstract Algebra I. D. Van Nostrand Company. ISBN 0-387-90122-1.
Jacobson, Nathan (2009). Basic algebra 1 (2nd ed.). Dover. ISBN 978-0-486-47189-1.

Outros artigos

Ligazóns externas

"Monoid". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
Weisstein, Eric W. "Monoid". MathWorld.
Monoid at PlanetMath.

[FOOTNOTEJacobson200931-2] Jacobson 2009, p. 31.

[1] Se ambos os dous $e 1$ e $e 2$ satisfán as ecuacións, daquela $e 1 = e 1 • e 2 = e 2$ .

[3] Proba: Fixamos un elemento $x$ do monoide. Dado que o monoide é finito, $x n = x m$ para algún $m > n > 0$ . Mais daquela, debido á cancelación temos que $x m - n = e$ onde $e$ é a identidade. Por tanto, $x • x m - n -1 = e$ , e así $x$ ten inversa.

[4] $f (x) * f (e M) = f (x * e M) = f (x)$ para todo $x$ en $M$ , cando $f$ é un homomorfismo de semigrupos e $e M$ é a identidade do dominio do seu monoide $M$ .

[a]

[1]

[b]

[c]