Teorema fundamental dos homomorfismos

En álxebra abstracta, o teorema fundamental dos homomorfismos, tamén coñecido como primeiro teorema do isomorfismo, relaciona a estrutura de dous obxectos entre os que se dá un homomorfismo, e do núcleo e a imaxe do homomorfismo.

Este teorema utilízase para demostrar os teoremas do isomorfismo .

Versión para grupos

Diagrama do teorema fundamental dos homomorfismos, onde f é un homomorfismo, N é un subgrupo normal de G, e temos que e define o elemento de identidade de G.

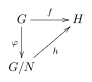
Dados dous grupos G e H e un homomorfismo de grupos f : G → H, sexa N un subgrupo normal en G e φ o homomorfismo sobrectivo natural G → G / N (onde G / N é o grupo cociente de G por N). Se N é un subconxunto de ker(f) entón existe un único homomorfismo h : G / N → H tal que f = h ∘ φ.

Noutras palabras, a proxección natural φ é universal entre os homomorfismos en G que mapean N no elemento identidade.

A situación descríbese no seguinte diagrama conmutativo:

h é inxectiva se e só se N = ker(f). Polo tanto, estabelecendo N = ker(f), obtemos inmediatamente o primeiro teorema do isomorfismo .

Podemos escribir o enunciado do teorema fundamental dos homomorfismos de grupos como "toda imaxe homomorfa dun grupo é isomorfa a un grupo cociente".

Proba

A demostración dedúcese a partir de dous feitos básicos sobre homomorfismos, a saber, a súa conservación da operación de grupo e a súa correspondencia entre os elementos identidade. Temos que demostrar que se $\phi :G\to H$ é un homomorfismo de grupos, entón:

1. ${\text{im}}(\phi )$ é un subgrupo $H$
2. $G/\ker(\phi )$ é isomorfo a ${\text{im}}(\phi )$

Proba de 1

A operación que se conserva por $\phi$ é a operación do grupo. Se $a,b\in {\text{im}}(\phi )$, entón existen elementos $a',b'\in G$ tal que $\phi (a')=a$ e $\phi (b')=b$. Para estes $a$ e $b$ temos $ab=\phi (a')\phi (b')=\phi (a'b')\in {\text{im}}(\phi )$ (posto que $\phi$ preserva a operación do grupo), e así, a propiedade de peche está satisfeita en ${\text{im}}(\phi )$. O elemento identidade $e\in H$ tamén está en ${\text{im}}(\phi )$ porque $\phi$ mapea o elemento de identidade de $G$ no identidade de $H$. Posto que cada elemento $a'$ en $G$ ten un inverso $(a')^{-1}$ tal que $\phi ((a')^{-1})=(\phi (a'))^{-1}$ (porque $\phi$ preserva a propiedade inversa tamén), temos un inverso para cada elemento $\phi (a')=a$ en ${\text{im}}(\phi )$, polo tanto, ${\text{im}}(\phi )$ é un subgrupo de $H$.

Proba de 2

Construír un mapa $\psi :G/\ker(\phi )\to {\text{im}}(\phi )$ por $\psi (a\ker(\phi ))=\phi (a)$. Este mapa está ben definido, pois se $a\ker(\phi )=b\ker(\phi )$, entón $b^{-1}a\in \ker(\phi )$ e así $\phi (b^{-1}a)=e\Rightarrow \phi (b^{-1})\phi (a)=e$ que dá $\phi (a)=\phi (b)$. Este mapa é un isomorfismo. $\psi$ é sobrexectivo sobre ${\text{im}}(\phi )$ por definición. Para mostrar a inxectividade, se $\psi (a\ker(\phi ))=\psi (b\ker(\phi ))$, entón $\phi (a)=\phi (b)$, o que implica $b^{-1}a\in \ker(\phi )$ así que $a\ker(\phi )=b\ker(\phi )$. Finalmente,

$$\psi ((a\ker(\phi ))(b\ker(\phi )))=\psi (ab\ker(\phi ))=\phi (ab)=\phi (a)\phi (b)=\psi (a\ker(\phi ))\psi (b\ker(\phi )),$$

por tanto $\psi$ preserva a operación do grupo. Por tanto $\psi$ é un isomorfismo entre $G/\ker(\phi )$ e ${\text{im}}(\phi )$, o que completa a proba.

Aplicacións

A versión de grupos do teorema fundamental dos homomorfismos pode ser usada para mostrar que dous grupos son isomorfos. A continuación móstranse dous exemplos.

Enteiros módulo n

Para cada $n\in \mathbb {N}$, considere os grupos $\mathbb {Z}$ e $\mathbb {Z} _{n}$ e un homomorfismo de grupo $f:\mathbb {Z} \rightarrow \mathbb {Z} _{n}$ definido por $m\mapsto m{\text{ mod }}n$ (ver aritmética modular). A continuación, considere o kernel de $f$, ${\text{ker}}(f)=n\mathbb {Z}$, que é un subgrupo normal en $\mathbb {Z}$. Existe un homomorfismo sobrexectivo natural $\varphi :\mathbb {Z} \rightarrow \mathbb {Z} /n\mathbb {Z}$ definido por $m\mapsto m+n\mathbb {Z}$. O teorema afirma que existe un isomorfismo $h$ entre $\mathbb {Z} _{n}$ e $\mathbb {Z} /n\mathbb {Z}$, ou noutras palabras $\mathbb {Z} _{n}\cong \mathbb {Z} /n\mathbb {Z}$. O diagrama conmutativo está ilustrado a continuación.

Teorema N/C

Sexa $G$ un grupo con subgrupo $H$. Sexan $C_{G}(H)$, $N_{G}(H)$ e ${\text{Aut}}(H)$ o centralizador, o normalizador e o grupo de automorfismos de $H$ en $G$, respectivamente. Daquela, o teorema N/C afirma que $N_{G}(H)/C_{G}(H)$ é isomorfo a un subgrupo de ${\text{Aut}}(H)$.

A proba

Podemos atopar un homomorfismo de grupos $f:N_{G}(H)\rightarrow {\text{Aut}}(H)$ definido por $g\mapsto ghg^{-1}$, para todo $h\in H$. Claramente, o kernel de $f$ é $C_{G}(H)$. Por tanto, temos un homomorfismo sobrexectivo natural $\varphi :N_{G}(H)\rightarrow N_{G}(H)/C_{G}(H)$ definido por $g\mapsto gC(H)$. O teorema fundamental dos homomorfismos afirma entón que existe un isomorfismo entre $N_{G}(H)/C_{G}(H)$ e $\varphi (N_{G}(H))$, que é un subgrupo de ${\text{Aut}}(H)$.

Outras versións

Teoremas similares son válidos para monoides, espazos vectoriais, módulos e, aneis.

Véxase tamén

Bibliografía

• Beachy, John A. (1999). "Theorem 1.2.7 (The fundamental homomorphism theorem)". Introductory Lectures on Rings and Modules. London Mathematical Society Student Texts 47. Cambridge University Press. p. 27. ISBN 9780521644075. 
• Grove, Larry C. (2012). "Theorem 1.11 (The Fundamental Homomorphism Theorem)". Algebra. Dover Books on Mathematics. Courier Corporation. p. 11. ISBN 9780486142135. 
• Jacobson, Nathan (2012). "Fundamental theorem on homomorphisms of Ω-algebras". Basic Algebra II. Dover Books on Mathematics (2nd ed.). Courier Corporation. p. 62. ISBN 9780486135212. 
• Rose, John S. (1994). "3.24 Fundamental theorem on homomorphisms". A course on Group Theory [reprint of the 1978 original]. Dover Publications, Inc., New York. pp. 44–45. ISBN 0-486-68194-7. MR 1298629. 

Outros artigos

• Categoría cociente.

Ligazóns externas

• Matthew Macauley The fundamental homomorphism theorem.