Función continua
En matemáticas, unha función continua é aquela para a que, intuitivamente, para puntos próximos do dominio prodúcense pequenas variacións nos valores da función; aínda que en rigor, nun espazo métrico significa o contrario, que pequenas variacións da función implican que deben estar próximos os puntos. Se a función non é continua, dise que é descontinua. Unha función continua de en é aquela cunha gráfica que pode debuxarse sen levantar o lapis do papel (máis formalmente a súa gráfica é un conxunto conexo).
A continuidade de funcións é un dos conceptos principais da análise matemática e da topoloxía.
Historia
[editar | editar a fonte]Unha primeira forma da definición (ε, δ) de continuidade foi dada por Bernard Bolzano en 1817. Augustin-Louis Cauchy definiu a continuidade de como segue: un incremento infinitamente pequeno da variable independente x sempre produce un cambio infinitamente pequeno da variable dependente y. Cauchy definiu cantitades infinitamente pequenas en termos de cantidades variables, e a súa definición de continuidade é paralela á definición infinitesimal empregada na actualidade. A definición e a distinción entre continuidade nun punto e continuidade uniforme foi dada por primeira vez por Bolzano na década de 1830 mais a súa obra non foi publicada ata cen anos despois. Como Bolzano,[1] Karl Weierstrass[2] negou a continuidade dunha función nun punto c a menos que estivese definida a ambos os lados de c, mais Édouard Goursat[3] permitía que unha función estivese definida só nun lado de c, e Camille Jordan[4] incluso se a función estaba definida só no punto c. Todas estas definicións non equivalentes de continuidade nun punto aínda se empregan.[5]
Eduard Heine achegou a primeira definición de continuidade uniforme en 1872, pero baseou estas ideas en traballos de Peter Gustav Lejeune Dirichlet de 1854.[6]
Funcións reais dunha variable real
[editar | editar a fonte]
Informalmente falando, unha función f definida sobre un intervalo I é continua se a curva que a representa, é dicir o conxunto dos puntos (x, f(x)), con x en I, está constituída por un trazo continuo, é dicir un trazo que non está roto, nin ten "ocos" nin "saltos", como na figura da dereita.
O intervalo I de x é o dominio de definición de f, definido como o conxunto dos valores de x para os cales existe f(x).
O intervalo J de y é o rango (tamén coñecido como imaxe) de f, o conxunto dos valores de y, tomados como y = f(x). Escríbese J = f(I). Notar que en xeral, non é igual que o codominio (só é igual se a función é sobrexectiva.)
O maior elemento de J chámase o máximo absoluto de f en I, e o menor valor de J é o seu mínimo absoluto no dominio I.
Continuidade dunha función nun punto
[editar | editar a fonte]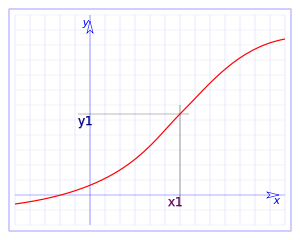
Unha función f é continua nun punto x0 no dominio da función se:
tal que para toda x no dominio da función:
Isto pódese escribir en termos de límites da seguinte maneira: Se x0 é punto de acumulación do dominio da función entón é continua en x0 se e só se . Cando x0 non é de acumulación do dominio, a función é continua nese punto.
No caso das aplicacións de en , e dunha maneira máis rigorosa dise que unha función f é continua nun punto x1 se existe f(x1), se existe o límite de f(x) cando x tende a x1 pola dereita, se existe o límite de (x) cando x tende a x1 pola esquerda, e ademais ambos coinciden con f(x1).[7]
Así pois, unha función f continua no punto x1 implica o seguinte: 1. Existe o límite pola dereita:
2. Existe o límite pola esquerda:
3. A función ten límite pola dereita e pola esquerda do punto x1
4. O límite pola dereita e o límite pola esquerda coinciden:
5. Se existen o límite pola dereita e pola esquerda e os seus valores coinciden, a función ten límite neste punto:
6. Existe f(x1):
7. O límite e o valor da función coinciden:
A función é continua nese punto. Unha función é continua nun intervalo se é continua en todos os seus puntos.

Se f(x1)= y1, a continuidade en x1 exprésase así:
Parafraseando, cando x se aproxima a x1, f(x) aproxímase a y1. Por definición dos límites, isto significa que para todo intervalo aberto J, centrado en y1, existe un intervalo aberto I, centrado en x1, tal que .
Se f ten un salto no punto, o teorema non se cumpre. En efecto, non todo intervalo I ao redor de x1 ten a súa imaxe nun intervalo J centrado en y1, cun raio inferior ao salto de f; non importa o pequeno que este intervalo sexa, hai valores de x do intervalo I ao redor de x1 que ten a súa imaxe nun intervalo K centrado en y2, sendo y1 e y2 valores distintos, isto é: x ten imaxes que saen de J.
A vantaxe desta definición é que se xeneraliza a calquera espazo topolóxico.
Continuidade lateral
[editar | editar a fonte]
Unha función f é continua pola esquerda no punto se o límite lateral pola esquerda e o valor da función no punto son iguais. É dicir:
como na figura.
Unha función f é continua pola dereita no punto se o seu límite lateral pola dereita e o valor da función no punto son iguais. É dicir:
Unha función f é continua nun punto se é continua pola esquerda e é continua pola dereita. Isto é:
Continuidade dunha función nun intervalo aberto: (a, b)
[editar | editar a fonte]Un valor c pertence a un intervalo aberto I, de extremo esquerdo a e extremo dereito b, representado I= (a, b) se:
Unha función f é continua nun intervalo aberto I= (a, b), se e só se a función é continua en todos os puntos do intervalo, é dicir:
Continuidade dunha función nun intervalo pechado: [a, b]
[editar | editar a fonte]Un valor c pertence a un intervalo pechado I, de extremo esquerdo a e extremo dereito b, representado I= [a, b] se:
Unha función f é continua nun intervalo pechado [a, b] se a función é continua no intervalo aberto (a, b) e é continua pola dereita da e continua pola esquerda de b:
Algunhas funcións continuas importantes
[editar | editar a fonte]
As funcións polinómicas, trigonométricas: seno e coseno, as exponenciais e as logarítmicas son continuas nos seus respectivos dominios de definición.
A parábola, como función polinómica, é un exemplo de función continua ao longo de todo o dominio real.
Na gráfica vese a función seno que é periódica, limitada e continua en todo o domino real. Dado o seu carácter periódico, con ver un só dos ciclos é suficiente para comprobar a continuidade, porque o resto dos ciclos son exactamente iguais.
Funcións definidas por intervalos
[editar | editar a fonte]
As funcións definidas para distintos intervalos de x poden ser descontinuas nos puntos de cambio de intervalo, por exemplo:
- A función parte enteira de x, E(x), onde E(x) é o maior número enteiro inferior ou igual a x, tal que:
- E(x) ≤ x < E(x) + 1.
A súa gráfica é unha sucesión de segmentos horizontais a distintas alturas. Esta función non é continua nos enteiros, pois os límites á esquerda e á dereita difiren dun, pero é continua nos segmentos abertos (n, n+1) onde é constante.
- Outra función definida por intervalo é a función signo.
Función racional
[editar | editar a fonte]
As funcións racionais son continuas nun intervalo axeitado. Un exemplo disto é a función inverso de x:
Esta función é unha hipérbole composta por dous tramos. x < 0 e x > 0. Como se ve, efectivamente é continua en todo o dominio porque non está definida en x= 0. Se se estende o dominio da función a ℝ (dándolle un valor arbitrario a f(0)) a función será descontinua.[8])
Teoremas sobre funcións continuas
[editar | editar a fonte]Estes son algúns dos teoremas máis importantes sobre funcións continuas.
- Teorema de Weierstrass: Se f é continua en entón presenta máximos e mínimos absolutos.
- Teorema de Bolzano: Se f é continua en e , entón tal que .
- Teorema do valor intermedio: Se f é continua en e entón tal que .
Anotación: Se f é unha función sobre un conxunto compacto entón, a función ten un máximo ou un mínimo. Sobre un conxunto aberto tense o seguinte contraexemplo: a función é continua sobre pero non é limitada.
Derivabilidade e continuidade
[editar | editar a fonte]As funcións derivables son continuas. Se unha función é derivable en x=a entón é continua en x=a. De modo que a continuidade é unha condición necesaria para a derivabilidade. É dicir, o conxunto das funcións derivables é parte das funcións continuas.
Cómpre notar que o recíproco non é válido; é dicir que nada se pode afirmar sobre a derivabilidade dunha función continua. Un exemplo claro desta situación é a función valor absoluto f(x)= |x| que aínda que é continua en todo o seu dominio non é derivable en x=0. Mesmo hai funcións continuas en todo ℝ pero non derivables en ningún punto (as funcións do movemento browniano verifican isto con probabilidade 1).
Clase de continuidade
[editar | editar a fonte]Unha función , dise que:
- é de clase cando é continua en todo o dominio
- é de clase se está definida en todo o dominio xunto coas súas derivadas até orde e todas elas son continuas.
- é de clase se ten derivadas continuas de calquera orde. As funcións deste tipo non son nercesariamente analíticas.
- é de clase se é a derivada no sentido das distribucións dunha función de clase .
- Unha función xeneralizada dise de clase se é a derivada k-ésima no sentido das distribucións dunha función de clase .
Calquera función polinómica dunha variable é unha función de clase . A función xeneralizada denominada delta de Dirac é unha función de clase xa que é a derivada segunda da función rampla que é continua, e a derivada primeira da función en esqueira de Heaviside que é de clase
Pódense dar exemplos que mostran que hai funcións de clase que non son de clase . Os exemplos clásicos son .
Funcións continuas en espazos topolóxicos
[editar | editar a fonte]Sexan e dous espazos topolóxicos. Unha aplicación dise que é continua se é un aberto de , calquera que sexa o aberto de . Esta é a continudade vista globalmente, a que segue é a continuidade nun punto do dominio.
Esta definición redúcese á definición ordinaria de continuidade dunha función se sobre e se considera a topoloxía inducida pola distancia euclidiana.
Coa mesma notación anterior, se , dise que é continua en cando se obtén que é unha veciñanza de , calquera que sexa a veciñanza de .
É inmediato entón comprobar que é continua se e só se é continua en , calquera que sexa este, é dicir, cando sexa continua en cada un dos puntos do seu dominio.
Funcións continuas sobre os números ordinais
[editar | editar a fonte]O termo función continua na parte da teoría de conxuntos que se refire aos números ordinais ten un sentido diferente ao referido ás funcións sobre espazos topolóxicos. Concretamente unha función F definida sobre a clase dos números ordinais é continua se para cada ordinal límite γ se cumpre a seguinte propiedade:
Notas
[editar | editar a fonte]- ↑ Bolzano, Bernard (1817). Rein analytischer Beweis des Lehrsatzes dass zwischen je zwey Werthen, die ein entgegengesetztes Resultat gewaehren, wenigstens eine reele Wurzel der Gleichung liege. Prague: Haase.
- ↑ Dugac, Pierre (1973). Eléments d'Analyse de Karl Weierstrass. Archive for History of Exact Sciences 10. pp. 41–176. doi:10.1007/bf00343406.
- ↑ Goursat, E. (1904). A course in mathematical analysis. Boston: Ginn. p. 2.
- ↑ Jordan, M.C. (1893). Cours d'analyse de l'École polytechnique 1 (2nd ed.). Paris: Gauthier-Villars. p. 46.
- ↑ Harper, J.F. (2016). Defining continuity of real functions of real variables. BSHM Bulletin: Journal of the British Society for the History of Mathematics. pp. 1–16. doi:10.1080/17498430.2015.1116053.
- ↑ Rusnock, P.; Kerr-Lawson, A. (2005). Bolzano and uniform continuity. Historia Mathematica 32. pp. 303–311. doi:10.1016/j.hm.2004.11.003.
- ↑ Lang, Serge (1997). Undergraduate analysis. Undergraduate Texts in Mathematics (2nd ed.). Berlín, Nova York: Springer-Verlag. ISBN 978-0-387-94841-6., section II.4
- ↑ Speck, Jared (2014). "Continuity and Discontinuity" (PDF). MIT Math. p. 3. Arquivado dende o orixinal (PDF) o 06-10-2016. Consultado o 2-9-2016.
Véxase tamén
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Función continua |
Bibliografía
[editar | editar a fonte]- Serge Lang (1990): Introdución al análisis Matemático , Wilmington Delaware.
- James R. Munkres (2002): Topología, Madrid.
Outros artigos
[editar | editar a fonte]- Clasificación de descontinuidades
- Lista de funcións matemáticas
- Derivación
- Continuo
- Continuidade uniforme
Ligazóns externas
[editar | editar a fonte]- Visual Calculus Arquivado 24 de setembro de 2011 en Wayback Machine. by Lawrence S. Husch, University of Tennessee (2001).


























![{\displaystyle \forall c\in I=[a,b]:\quad \lim _{x\to c}f(x)=f(c)\quad \land \quad \lim _{x\to a^{+}}f(x)=f(a)\quad \land \quad \lim _{x\to b^{-}}f(x)=f(b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/492ec2b396809c01662d6c821de2db488fdd1be3)


![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





































