Preorde
| Relacións binarias transitivas | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Todas as definicións requiren tacitamente que a relación homoxénea sexa transitiva: para todo se e entón |
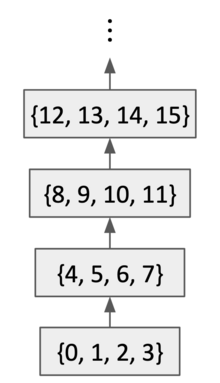
En matemáticas, especialmente na teoría da orde, unha preorde ou cuasiorde é unha relación binaria que é reflexiva e transitiva. O nome de preorde pretende suxerir que son ordes case parciais, mais non de todo, xa que non son necesariamente antisimétricas.
Un exemplo natural de preorde é a relación de división "x divide y" entre números enteiros, polinomios ou elementos dun anel conmutativo. Por exemplo, a relación de división é reflexiva pois cada número enteiro divídese a si mesmo. Mais a relación de división non é antisimétrica, porque divide e divide . É a esta preorde á que "máximo" e "mínimo" se refiren nas frases "máximo común divisor" e "mínimo común múltiplo" (agás que, para os enteiros, o máximo común divisor tamén é o máximo para a orde natural dos enteiros).
As preordes están estreitamente relacionadas coas relacións de equivalencia e as ordes parciais (non estritas). Ambas as dúas son casos especiais dunha preorde: unha preorde antisimétrica é unha orde parcial e unha simétrica unha relación de equivalencia. A maiores, unha preorde nun conxunto pódese definir equivalentemente como unha relación de equivalencia sobre , xunto cunha orde parcial sobre o conxunto da clase de equivalencia. Do mesmo xeito que as ordes parciais e as relacións de equivalencia, as preordes (nun conxunto non baleiro) nunca son asimétricas.
Como relación binaria, unha preorde pódese denotar como ou . En palabras, cando pódese dicir que b cobre a ou que a precede a b, ou que b redúcese en a. En ocasións, tamén se usa a notación ← ou →.
Definición
[editar | editar a fonte]Sexa unha relación binaria nun conxunto polo que, por definición, é algún subconxunto de . Entón chámase preorde ou quasiorde se é reflexiva e transitiva; é dicir, se cumpre:
- Reflexividade : para todos os e
- Transitividade : se para tódolos
Un conxunto que está equipado cunha preorde chámase conxunto preordenado (ou proset en inglés).
Preordes como ordes parciais en particións
[editar | editar a fonte]Dada unha preorde en pódese definir unha relación de equivalencia en tal que A relación resultante é reflexiva posto que a preorde é reflexiva; transitiva aplicando a transitividade de dúas veces; e simétrica por definición.
Usando esta relación, é posíbel construír unha orde parcial sobre o conxunto cociente da equivalencia, que é o conxunto de todas as clases de equivalencia de Se a preorde está indicada por entón é o conxunto de -ciclo clases de equivalencia: se e só se ou está nun -ciclo con . En todo caso, en é posíbel definir se e só se Que este está ben definido, é dicir, que a súa condición definitoria non depende dos representantes e que son escollidos, despréndese da definición de Verifícase facilmente que isto dá un conxunto parcialmente ordenado.
E viceversa, desde calquera orde parcial nunha partición dun conxunto é posíbel construír unha preorde en . Hai unha correspondencia un a un entre as preordes e os pares (partición, orde parcial).
Exemplo: Sexa unha teoría lóxica formal, que é un conxunto de proposicións con certas propiedades (os detalles pódense atopar no artigo sobre o tema). Por exemplo, podería ser unha Teoría de primeira orde (como a Teoría de conxuntos de Zermelo–Fraenkel) ou unha teoría máis sinxela como a teoría de orde cero. Unha das moitas propiedades de é que está pechada baixo conectivas lóxicas, polo que, por exemplo, se unha proposición implica loxicamente algunha proposición que se escribirá como e tamén como , entón necesariamente (por modus ponens). A relación é unha preorde en porque sempre se cumpre e sempre que e mantéñense, entón tamén o fai Alén diso, para calquera se e só se ; é dicir, dúas proposcións son equivalentes con respecto a se e só se son loxicamente equivalentes. Esta relación de equivalencia particular denótase habitualmente co seu propio símbolo especial , polo que este símbolo pódese usar en lugar de A clase de equivalencia dunha proposición denotada por consta de todas as proposicións que son loxicamente equivalentes a (é dicir, todas tal que ). A orde parcial en inducida por que tamén se denotará co mesmo símbolo caracterízase por se e só se onde a condición do lado dereito é independente da elección de representantes e das clases de equivalencia. Todo o que se dixo de ata agora tamén se pode dicir da súa relación inversa O conxunto preordenado é un conxunto dirixido porque se e se denota a proposición formada pola conxunción lóxica entón e onde O conxunto parcialmente ordenado é, en consecuencia, tamén un conxunto dirixido. Consulte Álxebra Lindenbaum–Tarski para obter un exemplo relacionado.
Relación con ordes parciais estritas
[editar | editar a fonte]Se a reflexividade substitúese pola irreflexividade (mentres se mantén a transitividade), obtemos a definición dunha orde parcial estrita sobre . Por este motivo, o termo preorde estrita úsase ás veces para unha orde parcial estrita. É dicir, esta é unha relación binaria sobre que satisfai:
- Irreflexividade ou antireflexividade: not para todos os é dicir, é falsa para todos os e
- Transitividade: se para todos os
Orde parcial estrita inducida por unha orde previa
[editar | editar a fonte]Calquera preorde dá lugar a unha orde parcial estrita definida por se e só se e non . Usando a relación de equivalencia introducida anteriormente, se e só se e así cúmprese o seguinte
Preordes inducidas por unha orde parcial estrita
[editar | editar a fonte]Usando a construción anterior, varios preordes non estritas poden producir a mesma preorde estrita así que sen máis información sobre como foi construída (tal coñecemento da relación de equivalencia por exemplo), quizais non sexa posíbel reconstruír a preorde orixinal non estrita a partir de
Exemplos
[editar | editar a fonte]Teoría de grafos
[editar | editar a fonte]- A relación de accesibilidade en calquera grafo dirixido (que pode conter ciclos) dá lugar a unha preorde, onde na preorde se e só se existe un camiño de x a y no grafo dirixido. Viceversa, cada preorde é a relación de accesibilidade dun grafo dirixido (por exemplo, o grafo que ten unha aresta de x a y para cada par (x, y) con ). Non obstante, moitos grafos diferentes poden ter a mesma orde de accesibilidade entre si. Do mesmo xeito, a accesibilidade dos grafos acíclicos dirixidos, grafos dirixidos sen ciclos, dá lugar a conxuntos parcialmente ordenados (preordes que satisfán unha propiedade de antisimetría adicional).
- A relación grafo menor tamén é unha orde previa.
Teoría de categorías
[editar | editar a fonte]- Unha categoría con como máximo un morfismo desde calquera obxecto x a calquera outro obxecto y é unha preorde. Esas categorías chámanse delgadas. Aquí os obxectos corresponden aos elementos de e hai un morfismo para os obxectos que están relacionados, cero en caso contrario. Neste sentido, as categorías "xeneralizan" as preordes permitindo máis dunha relación entre obxectos: cada morfismo é unha relación de preorde distinta.
- Alternativamente, un conxunto preordenado pódese entender como unha categoría enriquecida, enriquecida sobre a categoría
Outros
[editar | editar a fonte]- Todo espazo topolóxico finito dá lugar a unha preorde nos seus puntos mediante a definición se e só se x pertence a todas as veciñanzas de y. Toda preorde finita pódese formar deste xeito como a preorde de especialización dun espazo topolóxico. É dicir, hai unha correspondencia un a un entre topoloxías finitas e preordes finitas. No entanto, a relación entre espazos topolóxicos infinitos e as súas preordes de especialización non é un a un.
- Unha rede é unha preorde dirixida, é dicir, cada par de elementos ten un límite superior. A definición de converxencia a través de redes é importante na topoloxía, onde as preordes non se poden substituír por conxuntos parcialmente ordenados sen perder características importantes.
- A relación definida por se onde f é unha función nalgunha preorde.
- A relación definida por se existe algunha inxección de x a y. A inxección pode substituírse por sobrexección ou por calquera tipo de función de conservación da estrutura, como un homomorfismo de anel ou unha permutación.
- A relación de mergullo para ordes totais contábeis.
Exemplo de preorde total:
- Preferencia, segundo modelos comúns.
Construcións
[editar | editar a fonte]Toda relación binaria nun conxunto pódese ampliar a unha preorde en tomando o peche transitivo e o peche reflexivo, O peche transitivo indica a conexión do camiño se e só se hai un -camiño dende a
Preorde residual pola esquerda inducida por unha relación binaria
Dada unha relación binaria a composición complementada forma unha preorde chamada residual pola esquerda, (onde a barra "" non significa o "conxunto diferenza"), onde denota a relación inversa de e denota a relación complementaria de mentres denota composición de relacións.
Definicións relacionadas
[editar | editar a fonte]Se unha preorde tamén é antisimétrica, é dicir, e implica entón é unha orde parcial.
Por outra banda, se é simétrica, é dicir, se implica entón é unha relación de equivalencia.
Unha preorde é total se ou para todos os
Unha clase reservada é unha clase equipada cunha preorde. Todo conxunto é unha clase e, polo tanto, todo conxunto preordenado é unha clase preordenada.
Intervalo
[editar | editar a fonte]Para o intervalo é o conxunto de puntos x que satisfán e tamén escrito Contén polo menos os puntos a e b. Pódese optar por estender a definición a todos os pares . Os intervalos adicionais están todos baleiros.
Usando a relación estrita correspondente "", tamén se pode definir o intervalo como o conxunto de puntos x que satisfán e tamén escrito Un intervalo aberto pode estar baleiro aínda que
Tamén e poden definirse de xeito similar.
Notas
[editar | editar a fonte]Véxase tamén
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Preorde |
Bibliografía
[editar | editar a fonte]- Schmidt, Gunther, "Relational Mathematics", Encyclopedia of Mathematics and its Applications, vol. 132, Cambridge University Press, 2011, ISBN 978-0-521-76268-7
- Schröder, Bernd S. W. (2002). Ordered Sets: An Introduction. Boston: Birkhäuser. ISBN 0-8176-4128-9.
Outros artigos
[editar | editar a fonte]Ligazóns externas
[editar | editar a fonte]




































![{\displaystyle x\in [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c97e1e00ad3bbee9f19110b07b1d5919ff41159)



![{\displaystyle [x]\leq [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a78f45c685464633e52a4ca73a1bbc7e7f0ca480)

![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
![{\displaystyle [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f637a17dac262ee0fc8d58e31d08ca3ebe5a0fed)



















![{\displaystyle [A],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b5c411c8286b8fd5a4203b9b28f7483e3dd42b9)



![{\displaystyle [A]\Leftarrow [B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81ad0bf5548032e42220f44f7e239c6aae98f37b)

![{\displaystyle A\in [A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ed3c6736fef8d2f3a9bd405eef07d6283debf87)
![{\displaystyle B\in [B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee9b0fa0fe936466dbc7aed74f3a6301bda8f11b)




































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)










![{\displaystyle (a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6969e731af335df071e247ee7fb331cd1a57ae)