Conxunto parcialmente ordenado

Relacións binarias transitivas

	Simétrica	Antisimétrica	Conexa	Ben fundada	Ten joins	Ten meets	Reflexiva	Irreflexiva	Asimétrica

Relación de equivalencia	Si	Non	Non	Non	Non	Non	Si	Non	Non
Preorde (Cuasiorde)	Non	Non	Non	Non	Non	Non	Si	Non	Non
Orde parcial	Non	Si	Non	Non	Non	Non	Si	Non	Non
Preorde total	Non	Non	Si	Non	Non	Non	Si	Non	Non
Orde total	Non	Si	Si	Non	Non	Non	Si	Non	Non
Pre-Ben ordenada	Non	Non	Si	Si	Non	Non	Si	Non	Non
Cuasi-Ben ordenada	Non	Non	Non	Si	Non	Non	Si	Non	Non
Ben ordenada	Non	Si	Si	Si	Non	Non	Si	Non	Non
Retícula	Non	Si	Non	Non	Si	Si	Si	Non	Non
Semiretícula superior (join)	Non	Si	Non	Non	Si	Non	Si	Non	Non
Semiretícula inferior (meet)	Non	Si	Non	Non	Non	Si	Si	Non	Non
Orde estrita parcial	Non	Si	Non	Non	Non	Non	Non	Si	Si
Orde estrita feble	Non	Si	Non	Non	Non	Non	Non	Si	Si
Orde estrita total	Non	Si	Si	Non	Non	Non	Non	Si	Si
	Simétrica	Antisimétrica	Conexa	Ben fundada	Ten joins	Ten meets	Reflexiva	Irreflexiva	Asimétrica
Definicións, para todo $a,b$ e $S\neq \varnothing :$	${\begin{aligned}&aRb\\\Rightarrow {}&bRa\end{aligned}}$	${\begin{aligned}aRb{\text{ e }}&bRa\\\Rightarrow a={}&b\end{aligned}}$	${\begin{aligned}a\neq {}&b\Rightarrow \\aRb{\text{ ou }}&bRa\end{aligned}}$	${\begin{aligned}\min S\\{\text{existe}}\end{aligned}}$	${\begin{aligned}a\vee b\\{\text{existe}}\end{aligned}}$	${\begin{aligned}a\wedge b\\{\text{existe}}\end{aligned}}$	$aRa$	${\text{non }}aRa$	${\begin{aligned}aRb\Rightarrow \\{\text{non }}bRa\end{aligned}}$

Si indica que a columna da propiedade é sempre verdadeira no termo da fila (na esquerda de todo), mentres que

Non indica que a propiedade non está garantida en xeral (pode cumprirse ou non). Por exemplo, toda relación de equivalencia é simétrica, mais non necesariamente antisimétrica, está indicada por

Si na columna "Simétrica" e

Non na columna "Antisimétrica".

Todas as definicións requiren tacitamente que a relación homoxénea $R$ sexa transitiva: para todo $a,b,c,$ se $aRb$ e $bRc$ entón $aRc.$
Algunha definición dalgún termo pode requerir propiedades adicionais non recollidas na táboa.

En matemáticas, especialmente na teoría da orde, unha orde parcial nun conxunto é unha disposición tal que, para certos pares de elementos, un precede ao outro. A palabra parcial úsase para indicar que non todos os pares de elementos han de ser comparábeis; é dicir, pode haber pares para os que ningún elemento precede ao outro. As ordes parciais xeneralizan as ordes totais, nas que todo par é comparábel.

Formalmente, unha orde parcial é unha relación binaria homoxénea que é reflexiva, antisimétrica e transitiva. Un conxunto parcialmente ordenado (poset en inglés) é un par ordenado $P=(X,\leq )$ composto por un conxunto $X$ (chamado conxunto base de $P$ ) e unha orde parcial $\leq$ sobre $X$ .

Relacións de orde parcial

O termo orde parcial refírese xeralmente ás relacións de orde parcial reflexivas, referidas neste artigo como ordes parciais non estritas. Porén, algúns autores usan o termo para o outro tipo común de relacións de orde parcial, as relacións de orde parcial irreflexivas, tamén chamadas ordes parciais estritas. As ordes parciais estritas e as non estritas pódense poñer nunha correspondencia un a un, polo que para cada orde parcial estrita hai unha única orde parcial non estrita correspondente, e viceversa.

Ordes parciais

Unha orde parcial non estrita, ou débil,^[1] ou reflexiva,^[2] comunmente coñecida simplemente como orde parcial, é unha relación homoxénea ≤ nun conxunto $P$ que é reflexiva, antisimétrica e transitiva. É dicir, para todos $a,b,c\in P,$ debe satisfacer:

Reflexividade: $a\leq a$ , é dicir, cada elemento está relacionado consigo mesmo.
Antisimetría: se $a\leq b$ e $b\leq a$ entón $a=b$ .
Transitividade se $a\leq b$ e $b\leq c$ entón $a\leq c$ .

Unha orde parcial non estrita tamén se coñece como preorde antisimétrica.

Ordes parciais estritas

Un orde parcial estrita, ou forte,^[1] ou irreflexiva é unha relación homoxénea < nun conxunto $P$ que é irreflexiva, asimétrica e transitivoa; é dicir, cumpre as seguintes condicións para todos $a,b,c\in P:$

Irreflexividade : $\neg \left(a<a\right)$ , é dicir, ningún elemento está relacionado consigo mesmo (tamén chamada antirreflexivo).
Asimetría : se $a<b$ entón non $b<a$ .
Transitividade : se $a<b$ e $b<c$ entón $a<c$ .

A irreflexividade e a transitividade xuntas implican asimetría. A maiores, a asimetría implica irreflexividade. Noutras palabras, unha relación transitiva é asimétrica se e só se é irreflexiva.^[3] Lemma 1.1 (iv).</ref> Polo tanto, a definición é a mesma se omite a irreflexividade ou a asimetría (mais non ambas as dúas).

Unha orde parcial estrita tamén se coñece como preorde estrita asimétrica.

Correspondencia entre relacións de orde parcial estrita e non estrita

As ordes parciais estritas e non estritas nun conxunto $P$ están estreitamente relacionados. Unha orde parcial non estrita $\leq$ pódese converter nunha orde parcial estrita eliminando todas as relacións da forma $a\leq a;$ é dicir, a orde parcial estrita é o conxunto $<\;:=\ \leq \ \setminus \ \Delta _{P}$ onde $\Delta _{P}:=\{(p,p):p\in P\}$ é a relación de identidade sobre $P\times P$ e $\;\setminus \;$ indica a resta de conxuntos. No outro sentido, unha orde parcial estrita < sobre $P$ pódese converter nunha orde parcial non estrita agregando todas as relacións desa forma; é dicir, $\leq \;:=\;\Delta _{P}\;\cup \;<\;$ é unha orde parcial non estrita. Así, se $\leq$ é unha orde parcial non estrita, entón a orde parcial estrita correspondente < é o kernel irreflexivo dado por $a<b{\text{ if }}a\leq b{\text{ and }}a\neq b.$ Pola contra, se < é unha orde parcial estrita, entón a orde parcial non estrita correspondente $\leq$ é o peche reflexivo dado por: $a\leq b{\text{ if }}a<b{\text{ or }}a=b.$

Orde dual

A dual (ou oposta) $R^{\text{op}}$ dunha relación de orde parcial $R$ defínese por $R^{\text{op}}$ sendo a relación inversa de $R$ , é dicir $xR^{\text{op}}y$ se e só se $yRx$ . A dual dunha orde parcial non estrita é tamén non estrita, ^[4] e a dual dunha orde parcial estrita tamén estrita. A dual dunha relación dual é a relación orixinal.

Notación

Dado un conxunto $P$ e unha relación de orde parcial, normalmente a orde parcial non estrita $\leq$ , podemos estender de forma única a nosa notación para definir catro relacións de orde parcial $\leq ,$ $<,$ $\geq ,$ e $>$ , onde $\leq$ é unha relación de orde parcial non estrita sobre $P$ , $<$ é a relación de orde parcial estrita asociada en $P$ (o kernel irreflexivo de $\leq$ ), $\geq$ é o dual de $\leq$ , e $>$ é o dual de $<$ . En rigor, o termo conxunto parcialmente ordenado refírese a un conxunto con todas estas relacións definidas adecuadamente, mais na práctica, só hai que considerar unha única relación, $(P,\leq )$ ou $(P,<)$ , ou, en casos raros, as relacións non estritas e estritas entre si, $(P,\leq ,<)$ .^[5]

Cando se refire a ordes parciais, $\leq$ non debe tomarse como complemento de $>$ . A relación $>$ é a inversa do kernel irreflexivo de $\leq$ , que sempre é un subconxunto do complemento de $\leq$ , mais $>$ é igual ao complemento de $\leq$ se, e só se, $\leq$ é unha orde total.^[a]

Exemplos

Exemplos estándar de posets (conxuntos parcialmente ordenados) que aparecen en matemáticas inclúen:

Os números reais, ou en xeral calquera conxunto totalmente ordenado, ordenados pola relación estándar menor ou igual ≤, é unha orde parcial.
Sobre os números reais $\mathbb {R}$ , a relación usual menor que < é unha orde parcial estrita. O mesmo ocorre tamén coa relación usual maior que > en $\mathbb {R}$ .
Por definición, toda orde débil estrita é unha orde parcial estrita.
O conxunto de subconxuntos dun conxunto dado (o seu conxunto de partes) ordenados por inclusión (ver Fig. 1). Do mesmo xeito, o conxunto de secuencias ordenadas por subsecuencia, e o conxunto de cadeas ordenadas por subcadea.
O conxunto de números naturais equipados coa relación de divisibilidade. (ver Fig. 3 e Fig. 6)
O conxunto de vértices dun grafo acíclico dirixido ordenado por alcanzabilidade.
O conxunto de subespazos dun espazo vectorial ordenados por inclusión.

Ordes no produto cartesiano de conxuntos parcialmente ordenados

En orde crecente de forza, tres das posíbeis ordes parciais no produto cartesiano de dous conxuntos parcialmente ordenados son:

orde lexicográfica: (a, b) ≤ (c, d) se a < c ou ( a = c e b ≤ d );
a orde do produto: (a, b) ≤ (c, d) se a ≤ c e b ≤ d;
o peche reflexivo do produto directo das correspondentes ordes estritas: (a, b) ≤ (c, d) se (a < c e b < d) ou (a = c e b = d).

As tres poden definirse de xeito similar para o produto cartesiano de máis de dous conxuntos.

Aplicado a espazos vectoriais ordenados sobre o mesmo corpo, o resultado é en cada caso tamén un espazo vectorial ordenado.

Ver tamén ordes sobre o produto cartesiano de conxuntos totalmente ordenados.

Sumas de conxuntos parcialmente ordenados

Outra forma de combinar dous posets (disxuntos) é a suma ordinal (ou suma linear), ^[4] Z = X ⊕ Y, definida na unión dos conxuntos subxacentes X e Y pola orde a ≤_Z b se e só se:

a, b ∈ X con a ≤ _X b, ou
a, b ∈ Y con a ≤ _Y b, ou
a ∈ X e b ∈ Y.

Se dous posets están ben ordenados, entón tamén o está a súa suma ordinal.^[6]

Nocións derivadas

Os exemplos usan o poset $({\mathcal {P}}(\{x,y,z\}),\subseteq )$ constituído polo conxunto de todos os subconxuntos dun conxunto de tres elementos $\{x,y,z\},$ ordenados por inclusión do conxunto (ver Fig. 1).

a está relacionado con b cando a ≤ b. Isto non implica que b tamén estea relacionado con a, porque a relación non ten por que ser simétrica. Por exemplo, $\{x\}$ está relacionado con $\{x,y\},$ mais non ao revés.
a e b son comparábeis se a ≤ b ou b ≤ a. Se non se dá ningunha delas son non comparábeis. Por exemplo, $\{x\}$ e $\{x,y,z\}$ son comparábeis, mentres que $\{x\}$ e $\{y\}$ non o son.
Unha orde total ou orde linear é unha orde parcial baixo a cal cada par de elementos é comparábeis, é dicir, a tricotomía vale. Por exemplo, os números naturais coa súa orde estándar.
Unha cadea é un subconxunto dun poset que é un conxunto totalmente ordenado. Por exemplo, $\{\{\,\},\{x\},\{x,y,z\}\}$ é unha cadea.
Unha anticadea é un subconxunto dun poset no que non hai dous elementos distintos comparábeis. Por exemplo, o conxunto de conxuntos unitarios $\{\{x\},\{y\},\{z\}\}.$
Dise que un elemento a é estritamente menor que un elemento b, se a ≤ b e $a\neq b.$ Por exemplo, $\{x\}$ é estritamente menor que $\{x,y\}.$
Dise que un elemento a está cuberto por outro elemento b, escrito a ⋖ b (ou a <: b), se a é estritamente menor que b e non cabe un terceiro elemento c entre eles; formalmente: se tanto a ≤ b como $a\neq b$ son verdadeiras, e a ≤ c ≤ b é falsa para cada c con $a\neq c\neq b.$ Usando a orde estrita <, a relación a ⋖ b pódese reformular de forma equivalente como "a < b mais non a < c < b para calquera c". Por exemplo, $\{x\}$ está cuberto por $\{x,z\},$ mais non está cuberto por $\{x,y,z\}.$

Extrema

Hai varias nocións de elemento "maior" e "menor" nun poset $P,$ en particular:

Elemento maior e menor : Un elemento $g\in P$ é un elemento maior se $a\leq g$ para todo elemento $a\in P.$ Un elemento $m\in P$ é un elemento menor se $m\leq a$ para todo elemento $a\in P.$ Un poset só pode ter un elemento maior e un menor. No noso exemplo, o conxunto $\{x,y,z\}$ é o elemento maior e $\{\,\}$ é o elemento menor.
Elementos maximais e minimais: Un elemento $g\in P$ é maximal se non hai ningún elemento $a\in P$ tal que $a>g.$ Similarmente, un elemento $m\in P$ é minimal se non hai ningún elemento $a\in P$ tal que $a<m.$ Se un poset ten un elemento maior entón debe ser o único elemento maximal, mais sen elemento maior podería haber varios elementos maximais, e de forma similar para os elementos minimais. No noso examplo, $\{x,y,z\}$ e $\{\,\}$ son o elemento único maximal e minimal respectivamente. Se os eliminamos, daquela fican 3 elementos maximais e 3 elementos minimais (ver Fig. 5).
Elemento maiorante e minorante: Para un subconxunto A de P, un elemento x en P é un elemento maiorante de A se a ≤ x, para todo elemento a en A. En particular, x non necesita estar en A para ser elemento maiorante de A. Similarmente, un elemento x en P é un elemento minorante de A se a ≥ x, para todo elemento a en A. Un elemento maior de P é un elemento maiorante de P, e un elemento menor é un elemento minorante de P. No noso examplo, o conxunto $\{x,y\}$ é un elemento maiorante para a colección de elementos $\{\{x\},\{y\}\}.$

Como outro exemplo, considere os enteiros positivos, ordenados por divisibilidade: 1 é un elemento mínimo, xa que divide a todos os demais elementos; por outra banda este poset non ten un elemento maior. Este conxunto parcialmente ordenado nin sequera ten elementos máximais, xa que calquera g divide por exemplo a 2g, que é distinto del, polo que g non é máximal. Se se exclúe o número 1, mantendo a divisibilidade como orde nos elementos maiores que 1, entón o poset resultante non ten un elemento mínimal, pero calquera número primo é un elemento mínimal para el. Neste poset, 60 é un límite superior (aínda que non o mínimo deles ou supremo) do subconxunto $\{2,3,5,10\},$ que non ten límite inferior (xa que 1 non está no poset); por outra banda 2 é un límite inferior do subconxunto de potencias de 2, que non ten ningún límite superior. Se se inclúe o número 0, este será o elemento máis grande, xa que este é un múltiplo de todo número enteiro (ver Fig. 6).

Mapas entre conxuntos parcialmente ordenados

Fig. 7a Mapa con preservación de orde, mais non reflexivo de orde (posto que f(u) ≼ f(v), mais non u

\leq

v).

Fig. 7b Isomorfismo de orde entre os divisores de 120 (orde parcial por divisibilidade) e os subconxuntos pechados baixo divisor de {2, 3, 4, 5, 8} (orde parcial mediante inclusión de conxuntos)

Dado dous conxuntos parcialmente ordenados $(S, \leq)$ e $(T, ≼)$ , unha función $f:S\to T$ dise que conserva a orde, ou é monótona, ou isotona, se para todos os $x,y\in S,$ $x\leq y$ implica $f (x) ≼ f (y)$ . Se $(U, ≲)$ tamén é un conxunto parcialmente ordenado, e ambas as $f:S\to T$ e $g:T\to U$ preservan a orde, a súa composición $g\circ f:S\to U$ tamén conserva a orde.

Unha función $f:S\to T$ dise que unha reflexión de orde se para todos os $x,y\in S,$ $f (x) ≼ f (y)$ implica $x\leq y.$

Se $f$ conserva a orde e tamén reflicte a orde, entón chámase un mergullo de ordes de $(S, \leq)$ en $(T, ≼)$ .

Neste último caso, $f$ é necesariamente inxectiva, posto que $f(x)=f(y)$ implica $x\leq y{\text{ e }}y\leq x$ e á súa vez $x=y$ segundo a antisimetría de $\leq .$

Se un mergullo de orde $f:S\to T$ é bixectivo, chámase un isomorfismo de orde, e as ordes parciais $(S, \leq)$ e $(T, ≼)$ son isomorfas. As ordes isomorfas teñen estruturalmente similares Diagramas de Hasse (ver Fig. 7a).

Pódese demostrar que se existen os mapas $f:S\to T$ e $g:T\to U$ que conservan a orde tal que $g\circ f$ e $f\circ g$ producen a función de identidade en S e T, respectivamente, entón S e T son un isomorfismo de orde.^[4]

Por exemplo, un mapa $f:\mathbb {N} \to \mathbb {P} (\mathbb {N} )$ Desde o conxunto de números naturais (ordenados por divisibilidade) ata o conxunto de partes de números naturais (ordenados por inclusión de conxuntos) pódese definir levando cada número ao conxunto dos seus divisores primos. Conserva a orde: se $x$ divide $y$ , entón cada divisor primo de $x$ tamén é un divisor primo de $y$ . Porén, non é nin inxectivo (xa que asigna tanto 12 como 6 a $\{2,3\}$ ) nin reflicte a orde (xa que 12 non divide 6).

Polo contrario se definimos o mapa que asigna a cada número o conxunto dos seus divisores con potencia de primo, daquela temos un mapa $g:\mathbb {N} \to \mathbb {P} (\mathbb {N} )$ que conserva a orde e máis reflicte a orde e, polo tanto e un mergullo de orde. Non é un isomorfismo de orde (xa que, por exemplo, non asigna ningún número ao conxunto $\{4\}$ ), mais pódese facer un isomorfismo restrinxindo o seu codominio a $g(\mathbb {N} ).$ A Fig. 7b mostra un subconxunto de $\mathbb {N}$ e a súa imaxe isomorfa baixo $g$ . A construción de tal isomorfismo de orde nun conxunto de partes pódese xeneralizar a unha ampla clase de ordes parciais, chamadas retículas distributivas; ver o teorema de representación de Birkhoff .

Número de ordes parciais

A secuencia A001035 na OEIS dá o número de ordes parciais nun conxunto de n elementos etiquetados:

Número de relacións binarias dados n elementos de diferentes tipos
Elements	Calquera	Transitiva	Reflexiva	Simétrica	Preorde	Orde parcial	Preorde total	Orde total	Relación de equivalencia
0	1	1	1	1	1	1	1	1	1
1	2	2	1	2	1	1	1	1	1
2	16	13	4	8	4	3	3	2	2
3	512	171	64	64	29	19	13	6	5
4	65,536	3,994	4,096	1,024	355	219	75	24	15
n	2^n²		2ⁿ⁽ⁿ⁻¹⁾	2^n(n+1)/2			∑n k=0 k!S(n, k)	n!	∑n k=0 S(n, k)
OEIS	(secuencia A002416 na OEIS)	(secuencia A006905 na OEIS)	(secuencia A053763 na OEIS)	(secuencia A006125 na OEIS)	(secuencia A000798 na OEIS)	(secuencia A001035 na OEIS)	(secuencia A000670 na OEIS)	(secuencia A000142 na OEIS)	(secuencia A000110 na OEIS)

S(n, k) denota os Números de Stirling do segundo tipo.

O número de ordes parciais estritas é o mesmo que o de ordes parciais.

Se a conta se fai só ata isomorfismo, obtemos a secuencia 1, 1, 2, 5, 16, 63, 318,... (secuencia A000112 na OEIS) .

Subposets

Un poset $P^{*}=(X^{*},\leq ^{*})$ chámase subposet doutro poset $P=(X,\leq )$ sempre que $X^{*}$ é un subconxunto de $X$ e $\leq ^{*}$ é un subconxunto de $\leq$ . Esta última condición equivale ao requisito de que para calquera $x$ e $y$ en $X^{*}$ (e así tamén en $X$ ), se $x\leq ^{*}y$ entón $x\leq y$ .

Se $P^{*}$ é un subconxunto de $P$ e a maiores, para todos os $x$ e $y$ en $X^{*}$ , sempre que $x\leq y$ tamén temos $x\leq ^{*}y$ , entón chamamos a $P^{*}$ o subconxunto de $P$ inducido por $X^{*}$ , e escribimos $P^{*}=P[X^{*}]$ .

Extensión linear

Unha orde parcial $\leq ^{*}$ nun conxunto $X$ chámase extensión doutra orde parcial $\leq$ en $X$ se temos que para todos os elementos $x,y\in X,$ sempre que $x\leq y,$ tamén é o caso de que $x\leq ^{*}y.$ Unha extensión linear é unha extensión que tamén é unha orde linear (é dicir, total). Como exemplo clásico, a orde lexicográfica dos conxuntos totalmente ordenados é unha extensión linear da súa orde de produtos. Toda orde parcial pódese estender a unha orde total (principio de extensión da orde).^[7]

En informática, os algoritmos para atopar extensións lineares de ordes parciais (representados como as ordes de atinxibilidade dos grafos acíclicos dirixidos) chámanse ordenación topolóxica.

Na teoría de categorías

Cada poset (e cada conxunto preordenado) pode considerarse como unha categoría onde, para os obxectos $x$ e $y,$ hai como máximo un morfismo de $x$ a $y.$ Máis explicitamente, sexa hom(x, y) = {(x, y)} se x ≤ y (e noutro caso o conxunto baleiro) e $(y,z)\circ (x,y)=(x,z).$ Esas categorías ás veces chámanse categoría posetal.

Os posets son equivalentes entre si, se e só se son isomorfos. Nun poset, o elemento máis pequeno, se existe, é un obxecto inicial, e o elemento máis grande, se existe, é un obxecto terminal. A maiores, cada conxunto preordenado é equivalente a un poset. Finalmente, cada subcategoría dun poset é un isomorfismo pechado.

Ordes parciais en espazos topolóxicos

Se $P$ é un conxunto parcialmente ordenado ao que tamén se lle deu a estrutura dun espazo topolóxico, entón é habitual asumir que $\{(a,b):a\leq b\}$ é un subconxunto pechado do espazo produto topolóxico $P\times P.$ Baixo este suposto as relacións de orde parcial compórtanse ben nos límites no sentido de que se $\lim _{i\to \infty }a_{i}=a,$ e $\lim _{i\to \infty }b_{i}=b,$ e para todos $i,$ $a_{i}\leq b_{i},$ entón $a\leq b.$ ^[8]

Intervalos

Un conxunto convexo nun poset P é un subconxunto $I$ de P coa propiedade de que, para calquera x e y en $I$ e calquera z en P, se x ≤ z ≤ y, entón z tamén está en $I$ . Esta definición xeneraliza a definición de intervalos de números reais. Cando é posíbel a confusión cos conxuntos convexos de xeometría, úsase orde convexo en lugar de "convexo".

Unha subretícula convexa dunha retícula L é unha subretícula de L que tamén é un conxunto convexo de L. Toda subretícula convexa non baleira pode representarse de forma única como a intersección dun filtro e un ideal de L.

Un intervalo nun poset P é un subconxunto que se pode definir coa notación de intervalo:

Para a ≤ b, o intervalo pechado [a, b] é o conxunto de elementos x que satisfán a ≤ x ≤ b (é dicir, a ≤ x e x ≤ b). Contén polo menos os elementos a e b .
Usando a correspondente relación estrita "<", o intervalo aberto (a, b) é o conxunto de elementos x que satisfán a < x < b ( é dicir, a < x e x < b). Un intervalo aberto pode estar baleiro aínda que a < b. Por exemplo, o intervalo aberto (0, 1) nos números enteiros está baleiro xa que non hai ningún número enteiro $x$ tal que $0 < x < 1$ .
Os intervalos semiabertos [a, b) e (a, b] defínense de xeito similar.

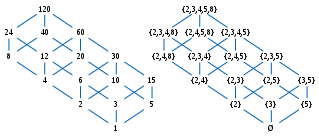
Sempre que a ≤ b non se cumpre, todos estes intervalos están baleiros. Todo intervalo é un conxunto convexo, mais a inversa non se cumpre; por exemplo, no poset dos divisores de 120, ordenados pola divisibilidade (ver Fig. 7b), o conxunto {1, 2, 4, 5, 8} é convexo, mais non é un intervalo.

Un intervalo $I$ está limitado se existen elementos $a,b\in P$ tal que $I \subseteq [a, b]$ . Todo intervalo que se pode representar en notación de intervalos está obviamente limitado, mais a inversa non é verdade. Por exemplo, sexa $P = (0, 1) \cup (1, 2) \cup (2, 3)$ como subconxunto dos números reais. O subconxunto (1, 2) é un intervalo limitado, mais non ten ínfimo nin supremo en P, polo que non se pode escribir en notación de intervalos usando elementos de P.

Un poset chámase localmente finito se cada intervalo limitado é finito. Por exemplo, os enteiros son localmente finitos baixo a súa orde natural. A orde lexicográfica sobre o produto cartesiano $\mathbb {N} \times \mathbb {N}$ non é localmente finito, xa que $(1, 2) \leq (1, 3) \leq (1, 4) \leq (1, 5) \leq ... \leq (2, 1)$ . Usando a notación de intervalo, a propiedade "a está cuberta por b" pódese reformular de forma equivalente como $[a,b]=\{a,b\}.$

Este concepto de intervalo nunha orde parcial non debe confundirse coa clase particular de ordes parciais coñecidas como ordes de intervalo.

Notas

↑ ^1,0 ^1,1 Wallis, W. D. (14 marzo 2013). A Beginner's Guide to Discrete Mathematics. Springer Science & Business Media. p. 100. ISBN 978-1-4757-3826-1.
↑ Simovici, Dan A.; Djeraba, Chabane (2008). "Partially Ordered Sets". Mathematical Tools for Data Mining: Set Theory, Partial Orders, Combinatorics. Springer. ISBN 9781848002012.
↑ Flaška, V.; Ježek, J.; Kepka, T.; Kortelainen, J. (2007). "Transitive Closures of Binary Relations I". Acta Universitatis Carolinae. Mathematica et Physica (Prague: School of Mathematics – Physics Charles University) 48 (1): 55–69. Lemma 1.1 (iv). This source refers to asymmetric relations as "strictly antisymmetric".
↑ ^4,0 ^4,1 ^4,2 Davey & Priestley (2002).
↑ Avigad, Jeremy; Lewis, Robert Y.; van Doorn, Floris (29 March 2021). "13.2. More on Orderings". Logic and Proof (Release 3.18.4 ed.). Arquivado dende o orixinal o 03 de abril de 2023. Consultado o 24 July 2021. Polo tanto, podemos pensar que cada orde parcial é realmente un par, que consiste nunha orde parcial feble e outra estrita asociada..
↑ P. R. Halmos (1974). Naive Set Theory. Springer. p. 82. ISBN 978-1-4757-1645-0.
↑ Jech, Thomas (2008) [1973]. The Axiom of Choice. Dover Publications. ISBN 978-0-486-46624-8.
↑ Ward, L. E. Jr (1954). "Partially Ordered Topological Spaces". Proceedings of the American Mathematical Society 5 (1): 144–161. doi:10.1090/S0002-9939-1954-0063016-5. hdl:10338.dmlcz/101379.

↑ Aquí pode ver unha proba: PartialOrders redundencies.pdf.

Véxase tamén

Bibliografía

Davey, B. A.; Priestley, H. A. (2002). Introduction to Lattices and Order (2nd ed.). New York: Cambridge University Press. ISBN 978-0-521-78451-1.
Deshpande, Jayant V. (1968). "On Continuity of a Partial Order". Proceedings of the American Mathematical Society 19 (2): 383–386. doi:10.1090/S0002-9939-1968-0236071-7.
Schmidt, Gunther (2010). Relational Mathematics. Encyclopedia of Mathematics and its Applications 132. Cambridge University Press. ISBN 978-0-521-76268-7.
Bernd Schröder (11 maio 2016). Ordered Sets: An Introduction with Connections from Combinatorics to Topology. Birkhäuser. ISBN 978-3-319-29788-0.
Stanley, Richard P. (1997). Enumerative Combinatorics 1. Cambridge Studies in Advanced Mathematics 49. Cambridge University Press. ISBN 0-521-66351-2.
Eilenberg, S. (2016). Foundations of Algebraic Topology. Princeton University Press.
Kalmbach, G. (1976). "Extension of Homology Theory to Partially Ordered Sets". J. Reine Angew. Math. 280: 134–156.

Outros artigos

Retícula (teoría da orde).

Ligazóns externas

2.2: Equivalence Relations, and Partial order LibreTexts mathematics.

[Wallis-1] 1,0 ^1,1 Wallis, W. D. (14 marzo 2013). A Beginner's Guide to Discrete Mathematics. Springer Science & Business Media. p. 100. ISBN 978-1-4757-3826-1.

[2] Simovici, Dan A.; Djeraba, Chabane (2008). "Partially Ordered Sets". Mathematical Tools for Data Mining: Set Theory, Partial Orders, Combinatorics. Springer. ISBN 9781848002012.

[Flaška_2007-3] Flaška, V.; Ježek, J.; Kepka, T.; Kortelainen, J. (2007). "Transitive Closures of Binary Relations I". Acta Universitatis Carolinae. Mathematica et Physica (Prague: School of Mathematics – Physics Charles University) 48 (1): 55–69. Lemma 1.1 (iv). This source refers to asymmetric relations as "strictly antisymmetric".

[FOOTNOTEDaveyPriestley2002-4] 4,0 ^4,1 ^4,2 Davey & Priestley (2002).

[5] Avigad, Jeremy; Lewis, Robert Y.; van Doorn, Floris (29 March 2021). "13.2. More on Orderings". Logic and Proof (Release 3.18.4 ed.). Arquivado dende o orixinal o 03 de abril de 2023. Consultado o 24 July 2021. Polo tanto, podemos pensar que cada orde parcial é realmente un par, que consiste nunha orde parcial feble e outra estrita asociada..

[7] P. R. Halmos (1974). Naive Set Theory. Springer. p. 82. ISBN 978-1-4757-1645-0.

[8] Jech, Thomas (2008) [1973]. The Axiom of Choice. Dover Publications. ISBN 978-0-486-46624-8.

[ward-1954-9] Ward, L. E. Jr (1954). "Partially Ordered Topological Spaces". Proceedings of the American Mathematical Society 5 (1): 144–161. doi:10.1090/S0002-9939-1954-0063016-5. hdl:10338.dmlcz/101379.

[6] Aquí pode ver unha proba: PartialOrders redundencies.pdf.

[1]

[2]

[3]

[4]

[5]

[a]

[6]

[7]

[8]