Retícula (teoría da orde)

Relacións binarias transitivas
Simétrica Antisimétrica Conexa Ben fundada Ten joins Ten meets Reflexiva Irreflexiva Asimétrica Relación de equivalencia  Si  Non  Non  Non  Non  Non  Si  Non  Non Preorde (Cuasiorde)  Non  Non  Non  Non  Non  Non  Si  Non  Non Orde parcial  Non  Si  Non  Non  Non  Non  Si  Non  Non Preorde total  Non  Non  Si  Non  Non  Non  Si  Non  Non Orde total  Non  Si  Si  Non  Non  Non  Si  Non  Non Pre-Ben ordenada  Non  Non  Si  Si  Non  Non  Si  Non  Non Cuasi-Ben ordenada  Non  Non  Non  Si  Non  Non  Si  Non  Non Ben ordenada  Non  Si  Si  Si  Non  Non  Si  Non  Non Retícula  Non  Si  Non  Non  Si  Si  Si  Non  Non Semiretícula superior (join)  Non  Si  Non  Non  Si  Non  Si  Non  Non Semiretícula inferior (meet)  Non  Si  Non  Non  Non  Si  Si  Non  Non Orde estrita parcial  Non  Si  Non  Non  Non  Non  Non  Si  Si Orde estrita feble  Non  Si  Non  Non  Non  Non  Non  Si  Si Orde estrita total  Non  Si  Si  Non  Non  Non  Non  Si  Si Simétrica Antisimétrica Conexa Ben fundada Ten joins Ten meets Reflexiva Irreflexiva Asimétrica Definicións, para todo $a,b$ e $S\neq \varnothing :$ ${\begin{aligned}&aRb\\\Rightarrow {}&bRa\end{aligned}}$ ${\begin{aligned}aRb{\text{ e }}&bRa\\\Rightarrow a={}&b\end{aligned}}$ ${\begin{aligned}a\neq {}&b\Rightarrow \\aRb{\text{ ou }}&bRa\end{aligned}}$ ${\begin{aligned}\min S\\{\text{existe}}\end{aligned}}$ ${\begin{aligned}a\vee b\\{\text{existe}}\end{aligned}}$ ${\begin{aligned}a\wedge b\\{\text{existe}}\end{aligned}}$ $aRa$ ${\text{non }}aRa$ ${\begin{aligned}aRb\Rightarrow \\{\text{non }}bRa\end{aligned}}$
Si indica que a columna da propiedade é sempre verdadeira no termo da fila (na esquerda de todo), mentres que  Non indica que a propiedade non está garantida en xeral (pode cumprirse ou non). Por exemplo, toda relación de equivalencia é simétrica, mais non necesariamente antisimétrica, está indicada por  Si na columna "Simétrica" e  Non na columna "Antisimétrica". Todas as definicións requiren tacitamente que a relación homoxénea $R$ sexa transitiva: para todo $a,b,c,$ se $aRb$ e $bRc$ entón $aRc.$ Algunha definición dalgún termo pode requerir propiedades adicionais non recollidas na táboa.

Unha retícula (en inglés lattice) é unha estrutura abstracta estudada nas subdisciplinas matemáticas da teoría da orde e da álxebra abstracta. Consiste nun conxunto parcialmente ordenado no que cada par de elementos ten un supremo único (tamén chamado límite superior mínimo ou join) e un ínfimo único (tamén chamado límite inferior máximo ou meet). Un exemplo é o conxunto de partes dun conxunto, parcialmente ordenado por inclusión, para o cal o supremo é a unión e o ínfimo é a intersección. Outro exemplo son os números naturais, parcialmente ordenados pola divisibilidade, para os que o supremo é o mínimo común múltiplo e o ínfimo é o máximo común divisor.

Definición

Unha retícula pode definirse tanto na teoría da orde como un conxunto parcialmente ordenado ou como unha estrutura alxébrica.

Como conxunto parcialmente ordenado

Un conxunto parcialmente ordenado (poset) $(L,\leq )$ chámase retícula se é á vez unha semiretícula join e meet, é dicir, cada subconxunto de dous elementos $\{a,b\}\subseteq L$ ten unha join (é dicir, límite superior mínimo, denotado por $a\vee b$ ) e dualmente un meet (é dicir, límite inferior máximo, denotado por $a\wedge b$). Esta definición fai $\,\wedge \,$ e $\,\vee \,$ operacións binarias. Ambas as operacións son monótonas en relación á orde dada: $a_{1}\leq a_{2}$ e $b_{1}\leq b_{2}$ implica que $a_{1}\vee b_{1}\leq a_{2}\vee b_{2}$ e $a_{1}\wedge b_{1}\leq a_{2}\wedge b_{2}.$

Como estrutura alxébrica

Unha retícula é unha estrutura alxébrica $(L,\vee ,\wedge )$, composta por un conxunto $L$ e dúas operacións binarias, conmutativas e asociativas $\vee$ e $\wedge$ en $L$ satisfacendo as seguintes identidades axiomáticas para todos os elementos $a,b\in L$ (ás veces chamadas leis de absorción): $$a\vee (a\wedge b)=a$$$$a\wedge (a\vee b)=a$$

As dúas identidades seguintes tamén son consideradas como axiomas, aínda que se deducen das dúas leis de absorción anteriores. Estas son as chamadas leis de idempotencia . $$a\vee a=a$$$$a\wedge a=a$$

Retícula limitada

Unha retícula limitada é unha retícula que ten a maiores un elemento maior (denotado por $1,$ ou por $\top$) e un elemento menor(denotado por $0$ ou por $\bot$), que satisfán $$0\leq x\leq 1\;{\text{ para todo }}x\in L.$$

Unha retícula limitada tamén se pode definir como unha estrutura alxébrica da forma $(L,\vee ,\wedge ,0,1)$ tal que $(L,\vee ,\wedge )$ é unha retícula, $0$ (o elemento menor) é o elemento identidade para a operación join $\vee ,$ e $1$ (o elemento maior) é o elemento identidade para a operación meet $\wedge .$$$a\vee 0=a.$$$$a\wedge 1=a.$$

Un conxunto parcialmente ordenado é unha retícula limitada se e só se cada conxunto finito de elementos (incluíndo o conxunto baleiro) ten un join e un meet.

Toda retícula pode ser mergullada nunha retícula limitada engadindo un elemento maior e un menor. A maiores, toda retícula finita non baleira está limitada, tomando o join (respectivamente o meet) de todos os elementos, denotado por ${\textstyle 1=\bigvee L=a_{1}\lor \cdots \lor a_{n}}$ (respectivamente ${\textstyle 0=\bigwedge L=a_{1}\land \cdots \land a_{n}}$ ) onde $L=\left\{a_{1},\ldots ,a_{n}\right\}$ é o conxunto de todos os elementos.

Conexión con outras estruturas alxébricas

As retículas teñen algunhas conexións coa familia de estruturas alxébricas de tipo grupo. Debido a que o join e o meet teñen a propiedade conmuttiva e asociativa, unha retícula pode ser vista como dous semigrupos conmutativos que teñen o mesmo dominio. Para unha retícula limitada, estes semigrupos son de feito monoides conmutativos. A lei de absorción é a única identidade definitoria que é propia da teoría de retículas. Unha retícula limitada tamén se pode pensar como un semianel conmutativo sen o axioma distributivo.

Exemplos

• 
  Imaxe.1: Subsconxuntos de $\{x,y,z\},$ baixo a inclusión de conxuntos.
• 
  Imaxe.2: Retícula de enteiros divisores de 60, ordenados por "divide a".
• 
  Imaxe.3: Reticula de particións de $\{1,2,3,4\},$ ordenado por "refina".
• 
  Imaxe.4:Retícula de enteiros positivos, ordenados por $\,\leq ,$
• 
  Imaxe.5: Retícula de pares de enteiros non negativos, ordenados compoñente a compoñente.

Exemplos de non retículas

Imaxe.6: Poset sen retícula: $c$ e $d$ non teñen límite superior común.

Imaxe.7: Poset sen retícula: $b$ e $c$ teñen límites superiores comúns $d,e,$ e $f,$ pero ningún deles é o límite superior mínimo.

Imaxe.8: Poset sen retícula: $a$ e $b$ teñen límites inferiores comúns $0,d,g,h,$ e $i,$ pero ningún deles é o límite inferior máis grande.

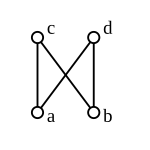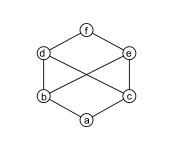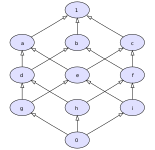Morfismos de retículas

Imaxe. 9: Mapa monótono $f$ entre retículas que non conserva nin joins nin meets, xa que $f(u)\vee f(v)=u^{\prime }\vee u^{\prime }=u^{\prime }$$\neq$$1^{\prime }=f(1)=f(u\vee v)$ e $f(u)\wedge f(v)=u^{\prime }\wedge u^{\prime }=u^{\prime }$$\neq$$0^{\prime }=f(0)=f(u\wedge v).$

A noción apropiada dun morfismo entre dúas retículas flúe facilmente da definición alxébrica dada previamente na parte superior do artigo. Dadas dúas retículas $\left(L,\vee _{L},\wedge _{L}\right)$ e $\left(M,\vee _{M},\wedge _{M}\right),$ un homomorfismo reticular de L a M é unha función $f:L\to M$ tal que para todos os $a,b\in L:$$$f\left(a\vee _{L}b\right)=f(a)\vee _{M}f(b),{\text{ e mesmo }}$$$$f\left(a\wedge _{L}b\right)=f(a)\wedge _{M}f(b).$$

En particular, un homomorfismo de retícula limitada (xeralmente chamado só "homomorfismo de retícula") $f$ entre dúas retículas limitadas $L$ e $M$ tamén debe ter as seguintes propiedades: $$f\left(0_{L}\right)=0_{M},{\text{ e }}$$$$f\left(1_{L}\right)=1_{M}.$$

Subretícula

Unha subretícula dunha retícula $L$ é un subconxunto de $L$ que é unha retícula coas mesmas operacións de join e meet que $L.$ É dicir, se $L$ é unha retícula e $M$ é un subconxunto de $L$ tal que para cada par de elementos $a,b\in M$ ambos os $a\wedge b$ e $a\vee b$ están en $M,$ entón $M$ é unha subretícula de $L.$

Unha subretícula $M$ dunha retícula $L$ é unha retícula convexa de $L,$ se $x\leq z\leq y$ e $x,y\in M$ implica que $z$ pertence a $M,$ para todos os elementos $x,y,z\in L.$

Propiedades das retículas

Agora introducimos unha serie de propiedades importantes que levan a clases especiais interesantes das retículas. Unha delas xa foi tratada co concepto de limitada.

Completude

Un poset chámase retícula completa se todos os seus subconxuntos teñen un join e un meet. En particular, toda retícula completa é unha retícula limitada. Mentres que os homomorfismos de retículas limitadas en xeral só conservan os joins e os meets finitos, para os homomorfismos de retículas completas é necesario preservar joins e meets arbitrarios.

"Reticula parcial" non é o contrario de "retícula completa"; máis ben, "retícula parcial", "retícula" e "retícula completa" son definicións cada vez máis restritivas.

Completude condicional

Unha retícula condicionalmente completa é unha retícula na que cada subconxunto non baleiro que ten un límite superior ten un join (é dicir, un límite superior mínimo). Esas retículas proporcionan a xeneralización máis directa do axioma de completude dos números reais. Unha retícula condicionalmente completa é unha retícula completa ou unha retícula completa sen o seu elemento máximo $1,$ o seu elemento mínimo $0,$ ou sen ambos os dous.

Distributividade

Imaxe. 11: A menor retícula non modular (e, polo tanto, non distributiva) N5.$b\leq c$, mais$b\vee (a\wedge c)=b$ e $(b\vee a)\wedge c=c$, polo que se incumpre a lei modular. Os elementos etiquetados tamén violan a ecuación da distributividade $c\wedge (a\vee b)=(c\wedge a)\vee (c\wedge b),$ mais satisfán o seu dual $c\vee (a\wedge b)=(c\vee a)\wedge (c\vee b).$

Imaxe. 10: Retícula máis pequena non distributiva (mais modular) M3.

Dado que as retícula veñen con dúas operacións binarias, é natural preguntarse se unha delas se distribúe sobre a outra, é dicir, se unha ou outra das seguintes leis duais cúmprese para cada tres elementos. $a,b,c\in L,$ :

Distributividade de $\vee$ sobre $\wedge$

$$a\vee (b\wedge c)=(a\vee b)\wedge (a\vee c).$$

Distributividade de $\wedge$ sobre $\vee$

$$a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c).$$

Unha retícula que satisfai o primeiro ou o segundo axioma, chámase retícula distributiva. As únicas retículas non distributivas con menos de 6 elementos chámanse M₃ e N₅; móstranse nas imaxes 10 e 11, respectivamente. Unha retícula é distributiva se e só se non ten unha subretícula isomorfa a M₃ ou N₅. Cada retícula distributiva é isomorfa a unha retícula de conxuntos (con unión e intersección como join e meet, respectivamente).

Modularidade

Para algunhas aplicacións a condición de distributividade é demasiado forte, e a seguinte propiedade máis débil adoita ser útil. Unha retícula $(L,\vee ,\wedge )$ é modular se, para todos os elementos $a,b,c\in L,$ ten a seguinte identidade: $(a\wedge c)\vee (b\wedge c)=((a\wedge c)\vee b)\wedge c.$ (Identidade modular)Esta condición é equivalente ao seguinte axioma: $a\leq c$ implica $a\vee (b\wedge c)=(a\vee b)\wedge c.$ (Lei modular)Unha retícula é modular se e só se non ten unha subretículas isomorfas a N₅ (mostrada na Fig. 11). A maiores das retículas distributivas, exemplos de retículas modulares son as retículas de submódulos dun módulo (polo tanto, modular), a retícula de ideais bilaterais dun anel e a retícula de subgrupos normais dun grupo.

Semimodularidade

Unha retícula finita é modular se e só se é semimodular tanto superiormente como inferiormente. Para unha retícula graduada, a semimodularidade (superior) é equivalente á seguinte condición na función de rango $r\colon$

$r(x)+r(y)\geq r(x\wedge y)+r(x\vee y).$

Continuidade e alxebricidade

Na teoría de dominios, é natural buscar aproximar os elementos nunha orde parcial mediante elementos "moito máis simples". Isto leva á clase de posets continuos, que consiste en posets onde todo elemento se pode obter como o supremo dun conxunto dirixido de elementos que están moi por debaixo do elemento. Se se pode restrinxir adicionalmente estes aos elementos compactos dun poset para obter estes conxuntos dirixidos, entón o poset é mesmo alxébrico. Ambos os conceptos pódense aplicar ás retículas do seguinte xeito:

• Unha retícula continua é unha retícula completa que é continua como poset.
• Unha retícula alxébrica é unha retícula completa que é alxébrica como poset.

Complementos e pseudocomplementos

Sexa $L$ unha retícula limitada co elemento maior 1 e o elemento menor 0. Dous elementos $x$ e $y$ de $L$ son complementos entre si, se e só se: $$x\vee y=1\quad {\text{ e }}\quad x\wedge y=0.$$

Condición de cadea de Jordan-Dedekind

Unha cadea de $x_{0}$ a $x_{n}$ é un conxunto $\left\{x_{0},x_{1},\ldots ,x_{n}\right\},$ onde $x_{0}<x_{1}<x_{2}<\ldots <x_{n}.$ A lonxitude desta cadea é n, ou un menos que o seu número de elementos. Unha cadea é máximal se $x_{i}$ cubre $x_{i-1}$ para todos os $1\leq i\leq n.$

Se para calquera par, $x$ e $y,$ onde $x<y,$ todas as cadeas maximais de $x$ a $y$ teñen a mesma lonxitude, entón dise que a retícula satisfai a condición da cadea de Jordan-Dedekind.

Importantes nocións teóricas de retículas

Definimos agora algunhas nocións da teoría da orde importantes para a teoría de retículas. No seguinte, denominamos como $x$ un elemento dalgunha retícula $L.$ Así $x$ chámase:

• Join irreducíbel se $x=a\vee b$ implica $x=a{\text{ ou }}x=b.$ para todos os $a,b\in L.$ Se $L$ ten un elemento menor $0,$ algúns autores requiren $x\neq 0$. Cando a primeira condición se xeneraliza a joins arbitrarios $\bigvee _{i\in I}a_{i},$ $x$ chámase join completamente irreducíbel (ou $\vee$-irreducíbel). A noción dual é meet irreducíbel ($\wedge$-irreducíbel). Por exemplo, na imaxe.2, os elementos 2, 3, 4 e 5 son join irreducíbeis, mentres que 12, 15, 20 e 30 son meet irreducibeis. Dependendo da definición, o elemento menor 1 e o elemento maior 60 poden considerarse ou non join irreducíbeis e meet irreducíbeis respectivamente. Na retícula de números reais coa orde habitual, cada elemento é join irreducíbele mais ningún é completamente join irreducíbel.
• Join primo se $x\leq a\vee b$ implica $x\leq a{\text{ ou }}x\leq b.$ De novo algúns autores requiren $x\neq 0$, aínda que isto é infrecuente. Isto tamén se pode xeneralizar para obter a noción join completamente primo. A noción dual é meet primo. Todo elemento join primo tamén é join irreducíbel, e todo elemento meet primo tamén é meet irreducíbel. A inversa cúmprese se $L$ é distributiva.

Teña $L$ un elemento menor 0. Un elemento $x$ de $L$ é un átomo se $0<x$ e non existe ningún elemento $y\in L$ tal que $0<y<x.$ Entón $L$ chámase:

• Atómica se para cada elemento distinto de cero $x$ de $L,$ existe un átomo $a$ de $L$ tal que $a\leq x;$
• Atomista se cada elemento de $L$ é un supremo de átomos.

Véxase tamén

Bibliografía

• Burris, Stanley N., and Sankappanavar, H. P., 1981. A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2.
• Jipsen, Peter, and Henry Rose, Varieties of Lattices, Lecture Notes in Mathematics 1533, Springer Verlag, 1992. ISBN 0-387-56314-8.

Textos elementais:

• Donnellan, Thomas, 1968. Lattice Theory. Pergamon.
• Grätzer, George, 1971. Lattice Theory: First concepts and distributive lattices. W. H. Freeman.

Texto contemporáneos introdutorios, algo máis duros que os anteriores:

• Davey, B. A.; Priestley, H. A. (2002). Introduction to Lattices and Order. Cambridge University Press. ISBN 978-0-521-78451-1. 

Outros artigos

• Join e meet
• Mapa de retículas
• Retícula ortocomplementeda
• Orde total
• Ideal (teoría da orde) e Filtro (matemáticas) (nocións duais)
• Retícula Euleriana
• Retícula de Post
• Retícula de Tamari

Ligazóns externas

• "Lattice-ordered group". Encyclopedia of Mathematics. EMS Press. 2001 [1994]. 
• Weisstein, Eric W. "Lattice". MathWorld. 
• J.B. Nation, Notes on Lattice Theory, course notes, revised 2017.
• Ralph Freese, "Lattice Theory Homepage".
• (secuencia A006966 na OEIS) Number of unlabeled lattices with n elements