Teoremas do isomorfismo

En matemáticas, en concreto álxebra abstracta, os teoremas do isomorfismo (tamén coñecidos como Teoremas de isomorfismo de Noether) son teoremas que describen a relación entre cocientes, homomorfismos e, subobxectos. Existen versións dos teoremas para grupos, aneis, espazos vectoriais, módulos, Álxebras de Lie, e outras estruturas alxébricas. En álxebra universal, os teoremas de isomorfismo poden ser xeneralizados ao contexto de álxebras e congruencias.

Historia

Os teoremas do isomorfismo foron formulados nalgunha xeneralidade para homomorfismos de módulos por Emmy Noether no seu artigo Abstrakter Aufbau der Idealtheorie en alxébrica Zahl - Und Funktionenkörpern, que foi publicado en 1927 en Mathematische Annalen. As versións menos xerais destes teoremas pódense atopar no traballo de Richard Dedekind e documentos anteriores de Noether.

Tres anos despois, B. l. van der Waerden publicou a súa influente Moderne Algebra, o primeiro libro de texto de álxebra abstracta que levou unha aproximación a este tema en grupos-aneis-corpos. Van der Waerden utilizou as conferencias de Noether sobre teoría de grupos e Emil Artín sobre álxebra, así como un seminario realizado por Artin, Wilhelm Blaschke, Otto Schreier, e o propio van der Waerden sobre ideais como as principais referencias.

Imos ver os teoremas de isomorfismo referidos aos grupos. Os teoremas refírense pola orde ou as veces polas letras A, B e C.

Primeiro teorema do isomorfismo

Diagrama do teorema fundamental sobre homomorfismos

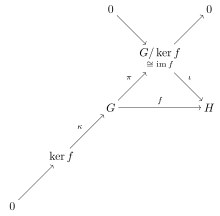
Sexan G e H grupos, e sexa f : G → H un homomorfismo. Entón:

O kernel de f é un subgrupo normal de G.
A imaxe de f é un subgrupo de H.
A imaxe de f é isomorfa ao grupo cociente G / ker(f).

En particular, se f é sobrexectivo entón H é isomorfo a G / ker(f).

Segundo teorema do isomorfismo

Diagrama para o segundo teorema punto 4. Os dous grupos cocientes (punteados) son isomorfos.

Sexa $G$ un grupo. Sexa $S$ un subgrupo de $G$ , e sexa $N$ un subgrupo normal de $G$ . Entón cúmprese o seguinte:

O produto $SN$ é un subgrupo de $G$ .
O subgrupo $N$ é un subgrupo normal de $SN$ .
A intersección $S\cap N$ é un subgrupo normal de $S$ .
Os grupos cocientes $(SN)/N$ e $S/(S\cap N)$ son isomorfos.

Tecnicamente, non é necesario que $N$ sexa un subgrupo normal, sempre que $S$ sexa un subgrupo do normalizador de $N$ en $G$ . Neste caso, $N$ non é un subgrupo normal de $G$ mais $N$ é aínda un subgrupo normal do produto $SN$ .

Unha aplicación do segundo teorema do isomorfismo é identificar os grupos lineares proxectivos, por exemplo, o grupo sobre a liña proxectiva complexa comeza facendo $G=\operatorname {GL} _{2}(\mathbb {C} )$ , o grupo de matrices complexas 2 × 2 invertíbeis, $S=\operatorname {SL} _{2}(\mathbb {C} )$ , o subgrupo de matrices de determinante 1, e $N$ o subgrupo normal de matrices escalares $\mathbb {C} ^{\times }\!I=\left\{\left({\begin{smallmatrix}a&0\\0&a\end{smallmatrix}}\right):a\in \mathbb {C} ^{\times }\right\}$ , con eses grupos temos $S\cap N=\{\pm I\}$ , onde $I$ é a matriz identidade e, $SN=\operatorname {GL} _{2}(\mathbb {C} )$ . Entón o segundo teorema do isomorfismo afirma que:

\operatorname {PGL} _{2}(\mathbb {C} ):=\operatorname {GL} _{2}\left(\mathbb {C} )/(\mathbb {C} ^{\times }\!I\right)\cong \operatorname {SL} _{2}(\mathbb {C} )/\{\pm I\}=:\operatorname {PSL} _{2}(\mathbb {C} )

Terceiro teorema do isomorfismo

Sexa $G$ un grupo, e $N$ un subgrupo normal de $G$ . Entón

Se $K$ é un subgrupo de $G$ tal que $N\subseteq K\subseteq G$ , entón $G/N$ ten un subgrupo isomorfo a $K/N$ .
Cada subgrupo de $G/N$ é da forma $K/N$ para algún subgrupo $K$ de $G$ tal que $N\subseteq K\subseteq G$ .
Se $K$ é un subgrupo normal de $G$ tal que $N\subseteq K\subseteq G$ , entón $G/N$ ten un subgrupo normal isomorfo a $K/N$ .
Cada subgrupo normal de $G/N$ é da forma $K/N$ para algún subgrupo normal $K$ de $G$ tal que $N\subseteq K\subseteq G$ .
Se $K$ é un subgrupo normal de $G$ tal que $N\subseteq K\subseteq G$ , entón o grupo cociente $(G/N)/(K/N)$ é isomorfo a $G/K$ .

As catro primeiras afirmacións adoitan subsumirse baixo o Cuarto teorema do isomorfismo que mostramos a continuación.

Cuarto teorema do isomorfismo

Sexa $G$ un grupo, e $N$ un subgrupo normal de $G$ . O homomorfismo da proxección canónica $G\rightarrow G/N$ define unha correspondencia bixectiva entre o conxunto de subgrupos de $G$ contendo $N$ e o conxunto dos (todos) subgrupos de $G/N$ . Baixo esta correspondencia, os subgrupos normais correspóndense con subgrupos normais.

Este teorema denomínanse tamén como o teorema da retícula, teorema de correspondencia.

Comentarios

O primeiro teorema do isomorfismo pode ser expresado en teoría das categoría coomo que a categoría de grupos é (epi normal, mono) factorizábel; noutras palabras, os epimorfismos normais e os monomorfismos forman un sistema de factorización para a categoría. Isto está capturado no diagrama conmutativo na marxe, que mostra os obxectos e morfismos cuxa existencia pode deducirse do morfismo $f:G\rightarrow H$ . O diagrama mostra que cada morfismo na categoría de grupos ten un kernel no sentido da teoría das categorías; o morfismo arbitrario f factoriza en $\iota \circ \pi$ , onde $\iota$ é un monomorfismo e $\pi$ é un epimorfismo (na categoría conormal, todos os epimorfismos son normais). Isto está representado no diagrama por un obxecto $\ker f$ e un monomorfismo $\kappa :\ker f\rightarrow G$ (os kernels son sempre monomorfismos), que completan a secuencia exacta curta que vai desde a parte inferior esquerda ata a parte superior dereita do diagrama. O uso da convención da secuencia exacta sálvanos de ter que debuxar os morfismos cero de $\ker f$ cara a $H$ e cara a $G/\ker f$ .

No segundo teorema do isomorfismo, o produto SN é o join de S e N na rede de subgrupos de G, mentres que a intersección S ∩ N é o meet.

O terceiro teorema do isomorfismo é xeneralizado polo lema nove para categorías abelianas e máis en xeral mapas entre obxectos.

Álxebra Universal

Para xeneralizar o visto anteriormente para grupos na álxebra universal, os subgrupos normais deben ser substituídos por relacións de congruencia.

Imos mostra un exemplo para o teorema fundamental do isomorfismo.

Primeiro teorema do isomorfismo na álxebra universal

Sexa $f:A\rightarrow B$ unha álxebra homomorfismo. Entón a imaxe de $f$ é unha subalxebra de $B$ , a relación dada por $\Phi :f(x)=f(y)$ (é dicir, o kernel de $f$ ) é unha congruencia sobre $A$ , e as álxebras $A/\Phi$ e $\operatorname {im} f$ son isomorfas. (Note que no caso dun grupo, $f(x)=f(y)$ se e só se $f(xy^{-1})=1$ , así cubrimos a noción de kernel usado na teoría de grupos neste caso.)

Notas

Véxase tamén

Bibliografía

Noether, Emmy, Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern, Mathematische Annalen 96 (1927) pp. 26–61
McLarty, Colin, "Emmy Noether's 'Set Theoretic' Topology: From Dedekind to the rise of functors". The Architecture of Modern Mathematics: Essays in history and philosophy (edited by Jeremy Gray e José Ferreirós), Oxford University Press (2006) pp. 211–35.
Jacobson, Nathan (2009). Basic algebra 1 (2nd ed.). Dover. ISBN 9780486471891.
Cohn, Paul M., Universal algebra, Chapter II.3 p. 57
Milne, James S. (2013). Group Theory. 3.13.
van der Waerden, B. I. (1994). Algebra 1 (9 ed.). Springer-Verlag.
Dummit, David S.; Foote, Richard M. (2004). Abstract algebra. Hoboken, NJ: Wiley. ISBN 978-0-471-43334-7.
Burris, Stanley; Sankappanavar, H. P. (2012). A Course in Universal Algebra (PDF). ISBN 978-0-9880552-0-9.
Scott, W. R. (1964). Group Theory. Prentice Hall.
Durbin, John R. (2009). Modern Algebra: An Introduction (6 ed.). Wiley. ISBN 978-0-470-38443-5.
Knapp, Anthony W. (2016). Basic Algebra (Digital second ed.).
Grillet, Pierre Antoine (2007). Abstract Algebra (2 ed.). Springer.
Rotman, Joseph J. (2003). Advanced Modern Algebra (2 ed.). Prentice Hall. ISBN 0130878685.
Hungerford, Thomas W. (1980). Algebra (Graduate Texts in Mathematics, 73). Springer. ISBN 0387905189.

Outros artigos

Ligazóns externas

Daniel Miranda, Universidade Federal do ABC, Álgebra Linear Avançada Teoremas de Isomorfismo.